【三平方の定理】を現場で活用する方法：距離・法長・直角設定

このブログは、建設現場で使われる直角三角形の公式【三平方の定理】について解説させていただきます。

三平方の定理とは

三平方の定理（ピタゴラスの定理）は、直角三角形における基本的な数学の法則です。

今から２５００年前、ギリシャの数学者ピタゴラスが発見したといわれています。

直角三角形の斜辺の長さを「a」、他の2辺の長さをそれぞれ「x」と「y」とした場合、次のような関係が成り立ちます。

$$a^2=x^2+y^2$$

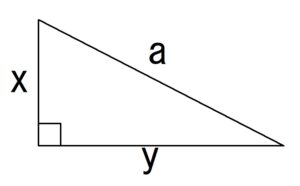
つまり、直角を挟む2辺の長さの二乗の和は、斜辺の長さの二乗に等しいという法則です。

建設現場での三平方の定理の活用

三平方の定理は、建設現場で非常に役立つツールとして広く利用されています。

その具体的な活用例をいくつかご紹介します。

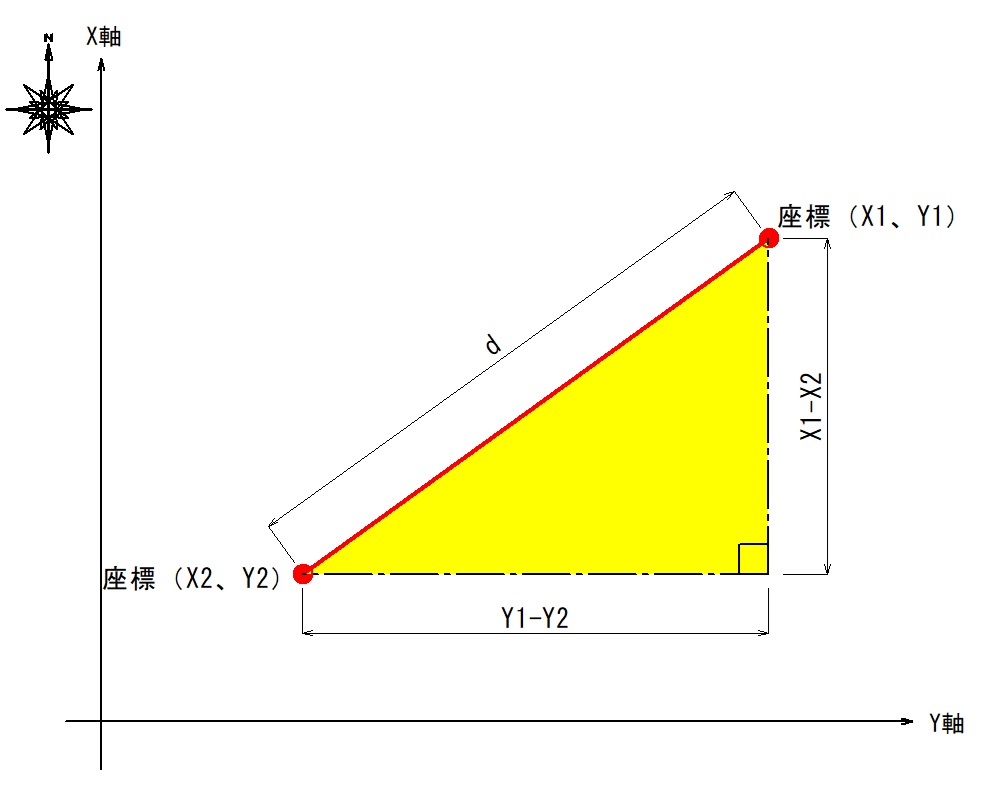
平面直角座標間の距離の計算

建設現場の測量では、平面直角座標系を使って位置を正確に設定します。

この座標間の距離を計算する際に、三平方の定理が用いられます。

例えば、ある2点の座標が(X1,Y1)と(X2​,Y2​)の場合、2点間の距離「d」は次の式で求められます。

$$d=\sqrt{(X1-X2)^2+(Y1-Y2)^2}$$

この計算によって、測量や施工に必要な正確な距離を求めることができます。

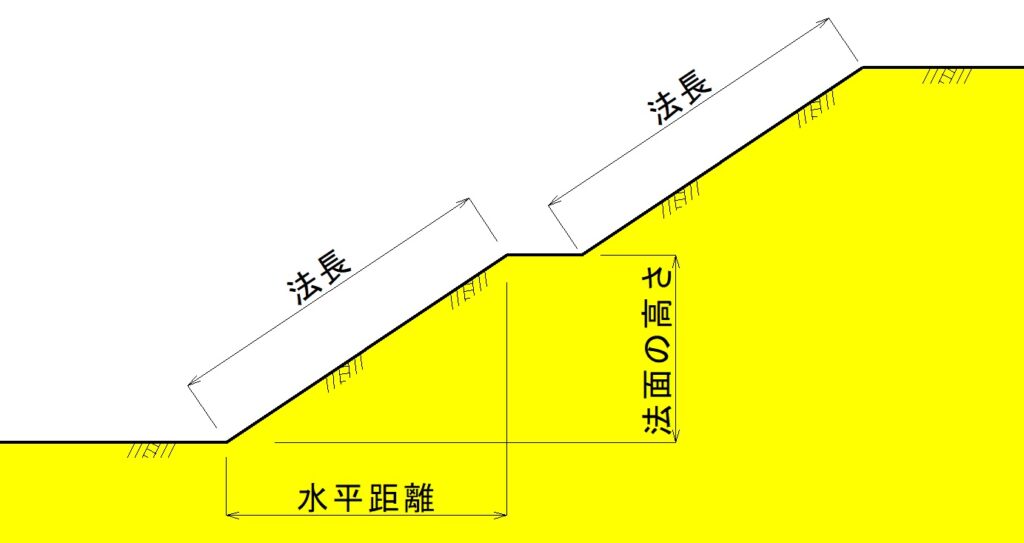
法面の長さ（法長）の計算

法面の長さ（法長）を計算する際にも三平方の定理が利用されます。

法面の高さ（垂直方向）と水平方向が分かれば、法面の長さ（法長）を簡単に求めることができます。

例えば、法面の高さが3.0m、水平距離が4.5mの場合、法長は次のように計算できます。

$$法長=\sqrt{3.0^2+4.5^2}$$

$$法長=\sqrt{9.0+20.25}$$

$$法長=\sqrt{29.25}$$

$$法長≒5.4ｍ$$

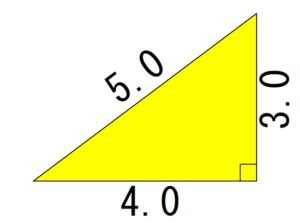
「3・4・5」の比を使った現地での直角設定

現場では、三平方の定理の特徴を利用して簡単に直角を出す方法も使われています。

特に、辺の比が「3：4：5」になる三角形は直角三角形であることが知られており、これを現地での作業に活用します。

例えば、直線上に3m、4mと測って、その間を5mの長さで結ぶことで、正確な直角を簡単に作ることができます。

$$5.0^2=3.0^2+4.0^2$$

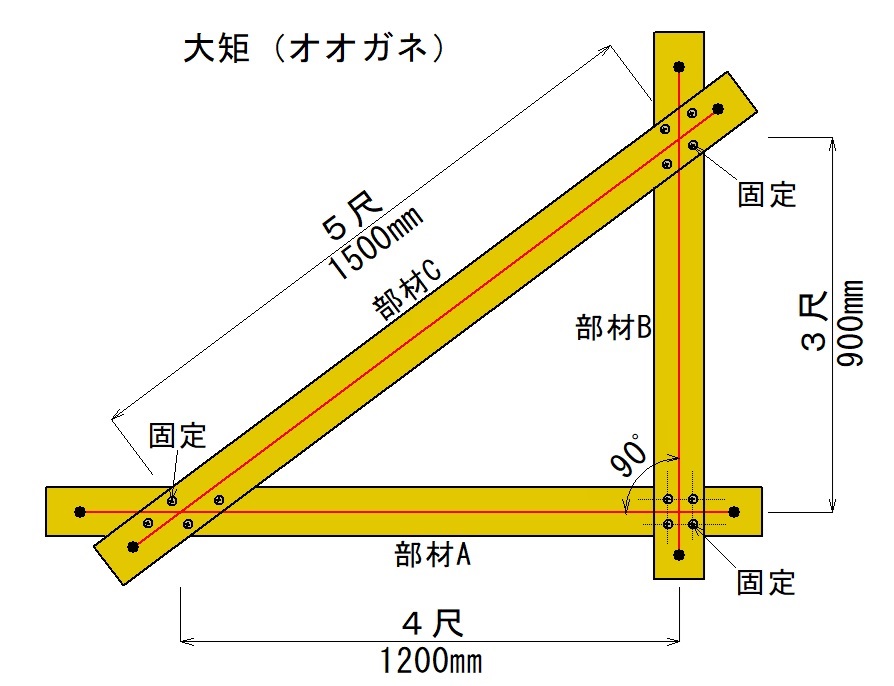
また、この「3：4：5」の比を活用した道具として【大矩（おおがね）】という大型の三角定規があり、測量や建築現場で利用されています。

この手法は、ピタゴラスが三平方の定理を発見するはるか前からバビロニアやエジプトで知られていました。

あわせて読みたい

富士山の頂上から見渡せる範囲を計算してみよう【三平方の定理】

まとめ

三平方の定理は、数学の基礎であると同時に、建設現場や測量の実務に欠かせない重要なツールです。

距離や高さ、斜面の長さの計算、直角の設定など、さまざまな場面で応用されています。

この定理を理解し、活用することで、作業の精度と効率が向上します。

ぜひ、現場でも積極的に活用してみてください！

にほんブログ村

にほんブログ村

にほんブログ村

川下　政明

土木施工管理技士

XInstagramYouTube

川下政明（かわしもまさあき）と申します。
土木施工管理歴３０年。
地場の建設会社に勤務しております。
1級土木、2級管工事、2級舗装、測量士、採石業務管理者を保有しております。
このブログは、工事現場に関する「施工管理」・「測量」・「HO_CAD」・「JW-CAD」・「パソコン」などについて発信しています。
参考にしていただけると嬉しいです。