2025.09.06 2025.09.07

後方交会法２点３点計算アプリ【スマホ・PC対応】

まさあき

記事内に商品プロモーションを含む場合があります

測量現場で「器械点の座標を求めたい」と思ったときに役立つのが後方交会法です。
しかし、実際に計算しようとすると…

式が複雑で手計算は大変
スマートフォンで手軽に計算したい
現場で素早く確認できない

こんな課題を感じたことはありませんか？

そこで今回、スマホやPCからそのまま使える「後方交会法・２点３点計算アプリ」を作成しました。
インストール不要、完全無料。ブラウザで開くだけで、現場ですぐに計算できます。

公開URLアプリの入手はここから
↓

後方交会法２点３点計算アプリ

Contents

アプリの概要
- 主な機能
２点モード（距離あり・円交点）
3点モード（角のみ：Tienstra法）
- 座標や角度を入力
- 「計算する」を押す
2点モードと3点モードの違い
杭打ち計算
まとめ

アプリの概要

このアプリは、後方交会法によって器械点（P）の座標を計算し、さらに杭打ち計算まで行えるWebアプリです。

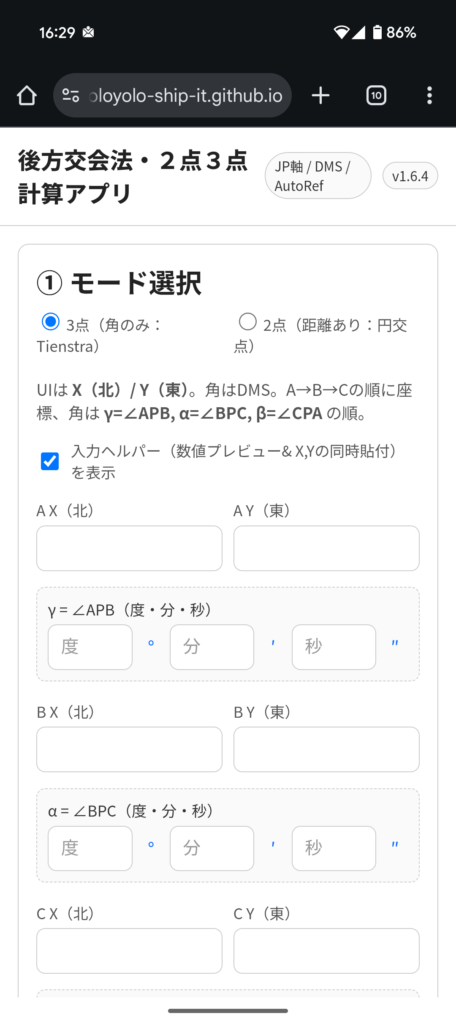
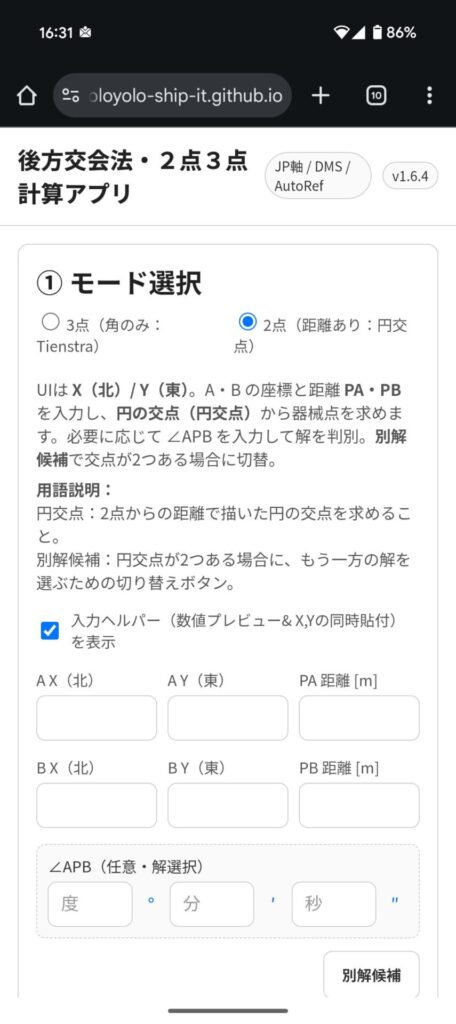
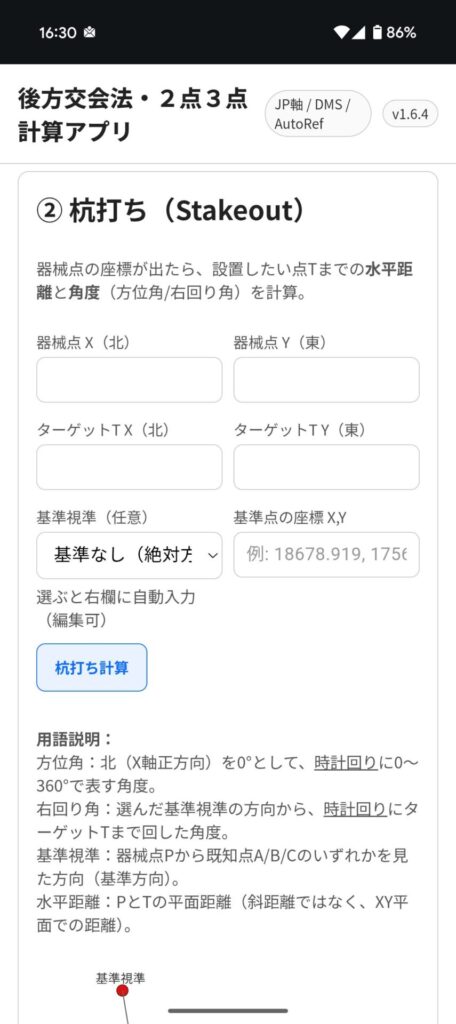
主な機能

2点モード（距離あり・円交点）
- 2点からの距離で円の交点を計算
- ∠APBを入力すれば正しい解を自動判別
- 「別解候補」ボタンで交点が2つ出た場合に切り替え可能
- エラー時は AB・PA+PB・|PA−PB| を自動表示 → 原因と調整の目安がわかる
3点モード（角のみ：Tienstra法）
- 3点A,B,Cと角度（γ=∠APB、α=∠BPC、β=∠CPA）を入力
- 器械点Pの座標を算出
- 内角チェックや角度の合計確認も可能
杭打ちモード
- 器械点からターゲット点Tまでの水平距離と角度（方位角・右回り角）を計算
- 基準視準をA,B,Cのいずれかから選択可能
- 現場での位置出し作業がスムーズに
入力ヘルパー機能
- X,Y座標を「12345.678, 98765.432」とコピペするだけで自動入力
- 入力した数値はプレビュー表示されるので、桁数の多い平面直角座標でも安心
略図・用語解説つき
- 2点モード・3点モード・杭打ち、それぞれに簡易図を表示
- 初心者でも座標と角度の関係がイメージしやすい

２点モード（距離あり・円交点）

あわせて読みたい

【後方交会法】座標点「２点」から器械点座標値の計算方法を解説

「2点モード（距離あり・円交点）」は、器械点から2つの既知点までの距離を使って器械点を求める方法です。

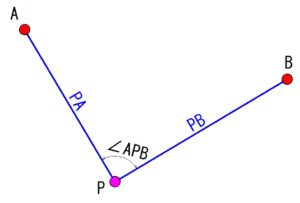
アプリでは交点の候補切替やエラーガイドまでサポートしてくれます。

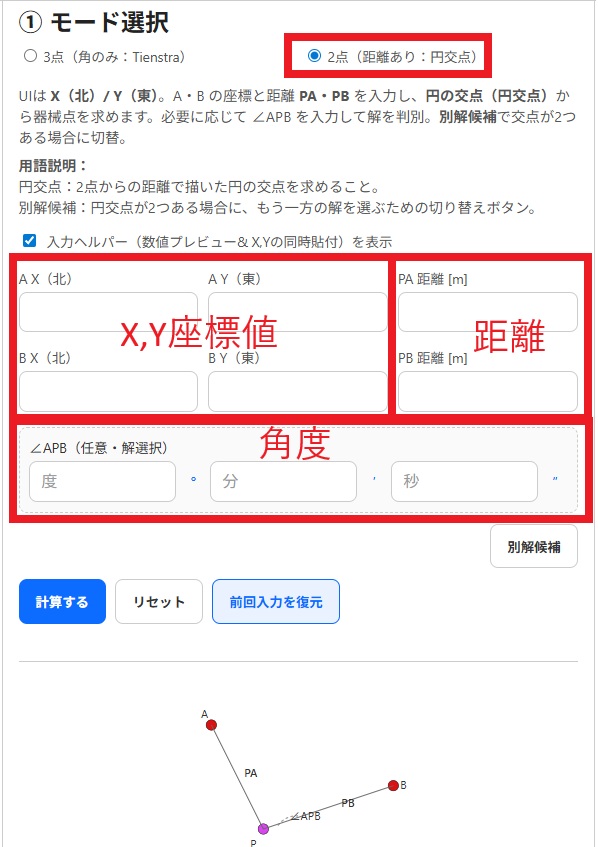
座標を入力

画面上部で「2点（距離あり：円交点）」を選びます。

既知点 A, B の座標（X=北, Y=東）を入力します。
テキストファイルからコピーした座標を「,（カンマ）」区切りで貼り付ければ自動で分割入力されます。

入力ヘルパー（数値プレビュー& X,Yの同時貼付）

このアプリでは、入力ヘルパー機能に「X座標（北）とY座標（東）をまとめて一度に貼り付けできる」仕組みを入れてあります。

測量データやCSVなどからコピーするとき、多くはスペースやカンマで区切られている形式ですよね。

12345.678　,　 98765.432

この値をそのままAXの入力欄にペーストします。
自動で「12345.678」をAXに、「98765.432」をAYに振り分けます。
AY欄にカーソルを移動してペーストし直す必要がありません。

距離や角度を入力

PA、PB（器械点からA,Bまでの水平距離）を入力します。

この状態で「計算する」をクリックしても器械点Pの座標を計算できますが、２つの答えになります。そこで ∠APB を入力すると、2つの候補から正しい交点を自動で判別します。

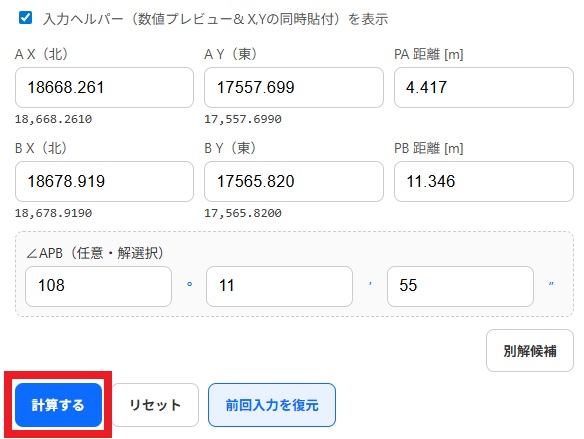
「計算する」を押す

器械点Pの座標が即座に表示されます。
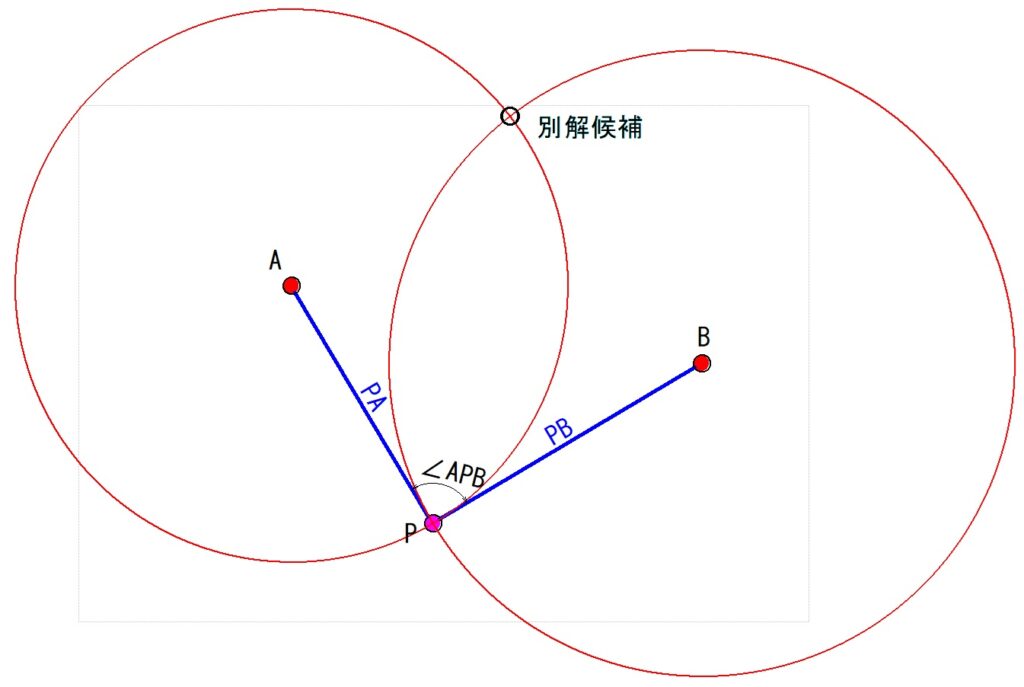
→ 入力した座標と距離をもとに、自動で計算します。
計算の仕組み：円の交点
→ AとBを中心に、半径PA・PBの円を描くと、その交点が器械点Pとなります。
交点は2つある場合があります。
→ どちらが正しい器械点かを判定する必要があります。
∠APBを入力した場合
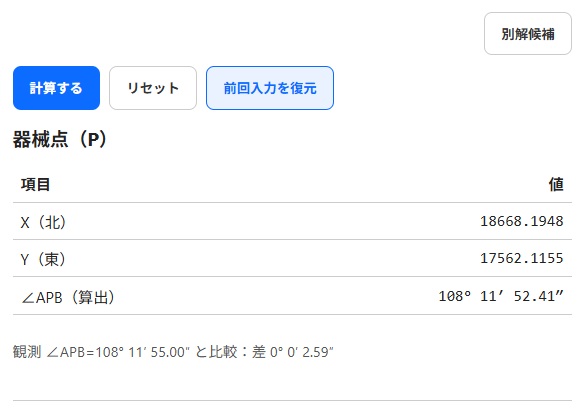
→ 2つの候補から自動で正しい交点を判別します。
角度チェックも可能
→ 計算上の角度と、実際に観測した角度の差を表示するので、観測値との整合性を確認できます。

エラーが出る場合

AB が PA+PB より大きい → 器械点が届かない（2円が離れている）
AB が |PA−PB| より小さい → 一方の円が他方を内包して交点ができない
A と B が同一点 → 計算不能

アプリでは、AB, PA+PB, |PA−PB| の値と原因・調整目安を表示するので、「なぜ計算できないか」が一目でわかります。

公開URLアプリの入手はここから
↓

後方交会法２点３点計算アプリ

3点モード（角のみ：Tienstra法）

あわせて読みたい

【後方交会法】座標点「3点」から器械点座標値の計算方法を解説

「3点モード（角のみ：Tienstra法）」は、既知点が3つ（A,B,C）あり、それらの角度を観測して器械点Pの座標を求める方法です。

Tienstra法とは？

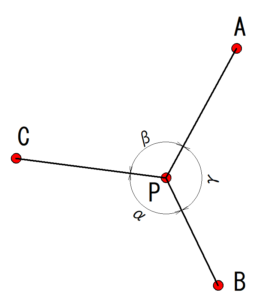
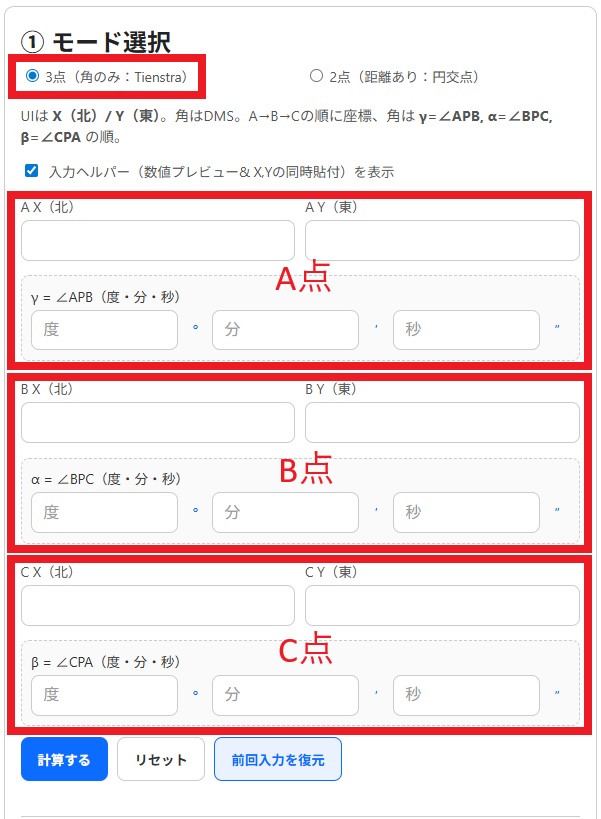
Tienstra（ティエンストラ）式は、後方交会法の代表的な計算式のひとつで、「角度3つと座標3つがあれば器械点Pを求められる」というシンプルな方法です。

計算式は少し複雑ですが、アプリが自動で処理してくれます。
手計算や電卓でやると大変なものを、ワンクリックで算出できるのが大きなメリットです。

座標や角度を入力

A,B,Cの座標（X=北, Y=東）を入力します。

γ=∠APB, α=∠BPC, β=∠CPA を「度・分・秒（DMS）」で入力します。

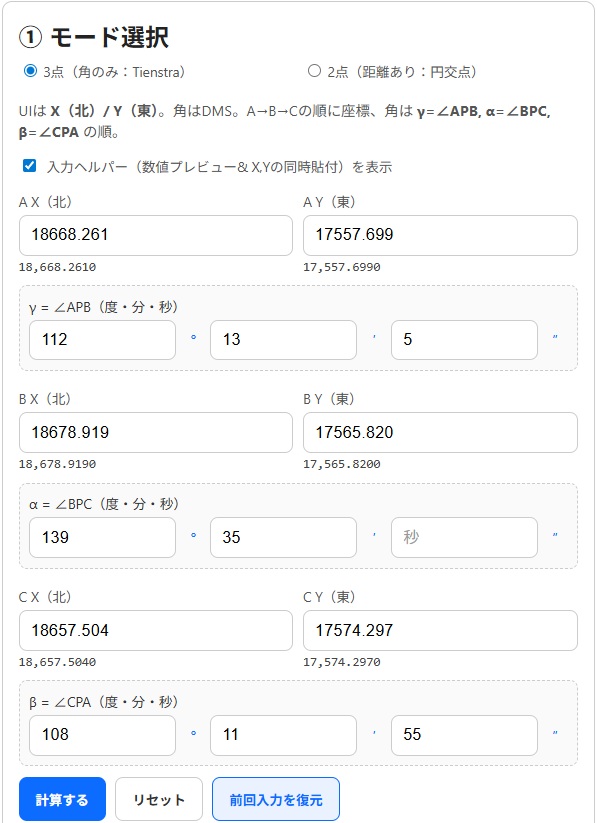
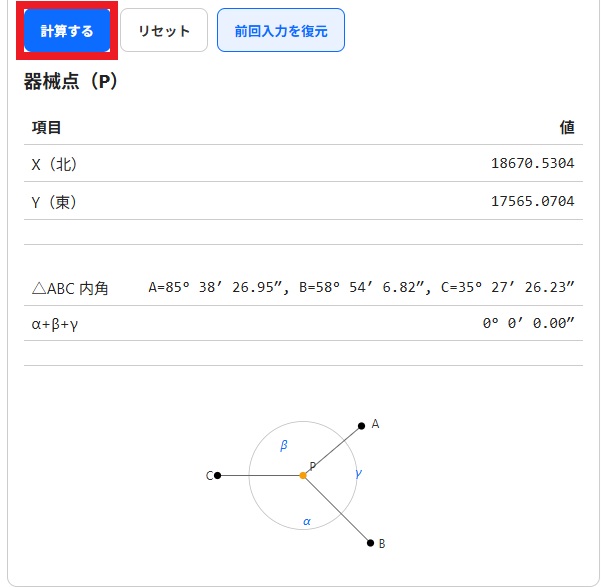
「計算する」を押す

「計算する」を押すと、器械点Pの座標X,Y が表示されます。

さらにアプリは三角形ABCの内角チェックも行い、観測角度の合計（α+β+γ）が360°（０°）に近いかどうか確認できます。

エラー例

α+β+γ の合計が360°にならない
角度の割当て誤り（γ,α,βを間違える）
A,B,Cが一直線に近い → 数値が不安定

2点モードと3点モードの違い

このアプリ【後方交会法】には「2点モード（距離あり・円交点）」と「3点モード（角のみ：Tienstra法）」があるので、どちらを使えばいいのか分かりやすいように、比較表にまとめました。

項目	2点モード（距離あり：円交点）	3点モード（角のみ：Tienstra法）
必要な既知点	2点（A・B）	3点（A・B・C）
観測データ	PA・PB（P→A, P→Bの水平距離）＋任意で ∠APB	角度：γ=∠APB、α=∠BPC、β=∠CPA（DMS）
計算の原理	PA・PB を半径とする 2円の交点を求める	Tienstra式（角度の三角比による演算）
結果	P の座標（X,Y）※交点が2つ出る場合あり	P の座標（X,Y）※解は一意
エラー例	・AB > PA+PB（円が離れて交わらない）・AB < \|PA−PB\|（一方が他方を内包）・AB ≒ PA+PB または AB ≒ \|PA−PB\|（接して不安定）・A と B が同一点／極端に近接・PA・PB が水平距離でない等の入力ミス	・観測角の合計 α+β+γ ≠ 360° ・角の割当て誤り（γ=∠APB, α=∠BPC, β=∠CPA の取り違え）・A, B, C がほぼ一直線（△ABC が極小）で数値不安定・DMSの桁ズレ／度分秒入力ミス
アプリのサポート	「別解候補」で交点切替／エラー原因と調整目安を自動表示	△ABC 内角チェック／α+β+γ の合計確認
利用シーン	既知点が2つあり距離測定が容易	既知点が3つ見えて角度観測が主体

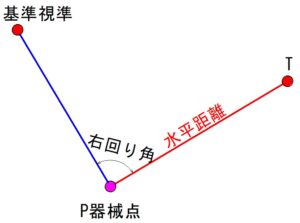
杭打ち計算

「杭打ちモード」は、器械点（P）の座標が求まったあとに、現地で新しい点を設置するための機能です。
具体的には、器械点Pからターゲット点Tまでの

水平距離（m）
角度（方位角・右回り角）

を計算します。
これにより、現場で正確にターゲット点を杭打ちできます。

アプリでの操作手順

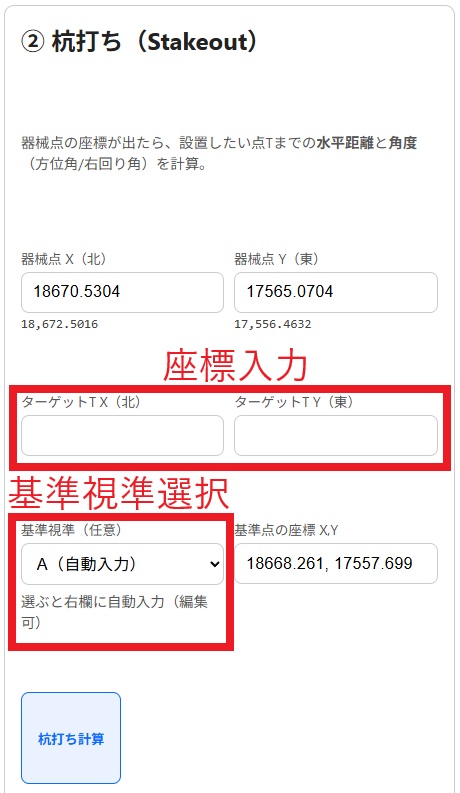
ターゲット点Tの座標を入力
設置したい点TのX（北）、Y（東）を入力します。
器械点の座標は、2点モード or 3点モードで計算した結果を、自動的に入力欄に反映されます。
基準視準を選択
A・B・Cのいずれかを基準点として指定できます。
選ぶと、その基準点の座標が自動で入力されます。
このとき「基準方向に対して右回りに何度か」でターゲット点Tを導けます。