座標計算【角度・距離】を計算しよう｜逆トラ・逆打ち

今回のブログでは、平面直角座標を使った「水平角度」と「水平距離」を計算していきます。

例として下の平面図を用意しました。

№２までの「水平角度」と「水平距離」を計算して測点を復旧しましょう。

1. 既知点「T-1」にトータルステーションを据付けます。
2. 既知点「T-2」を視準し、水平角度を0セット(0°0′0″）します。
3. №2までの水平距離と水平角度を計算します。
4. 計算した水平角度と水平距離で№2を復旧します。

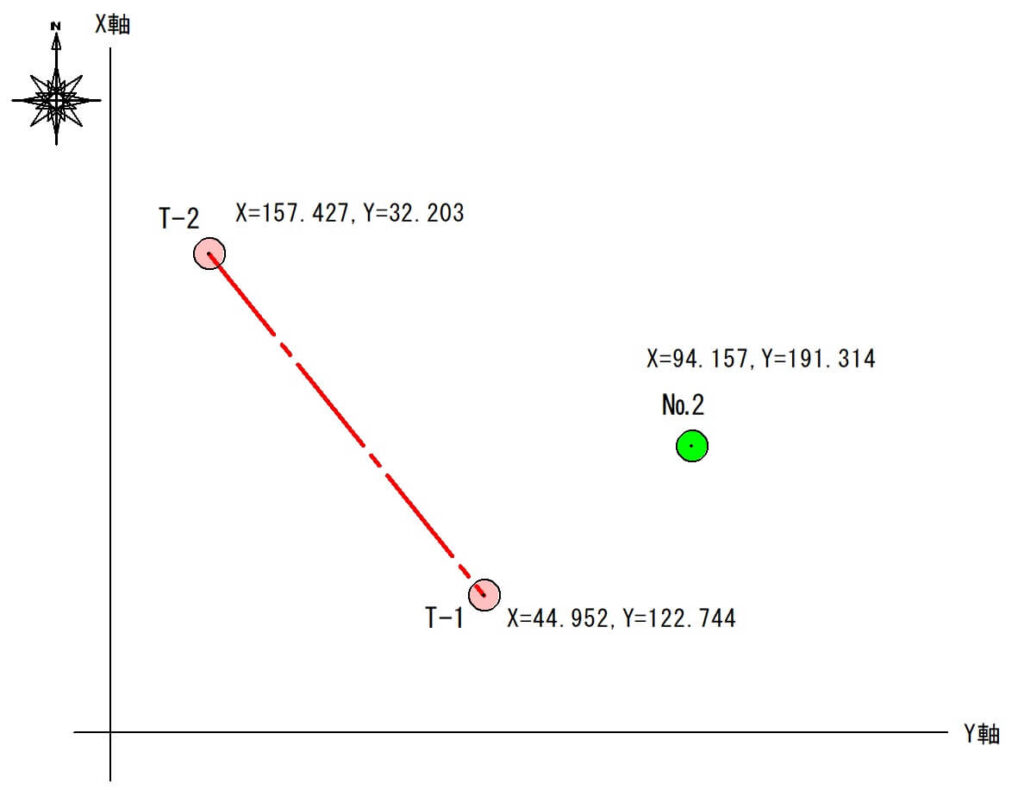
T-1座標：X＝44.952、Y＝122.744
T-2座標：X＝157.427、Y＝32.203
№2座標：X=94.157、Y＝191.314

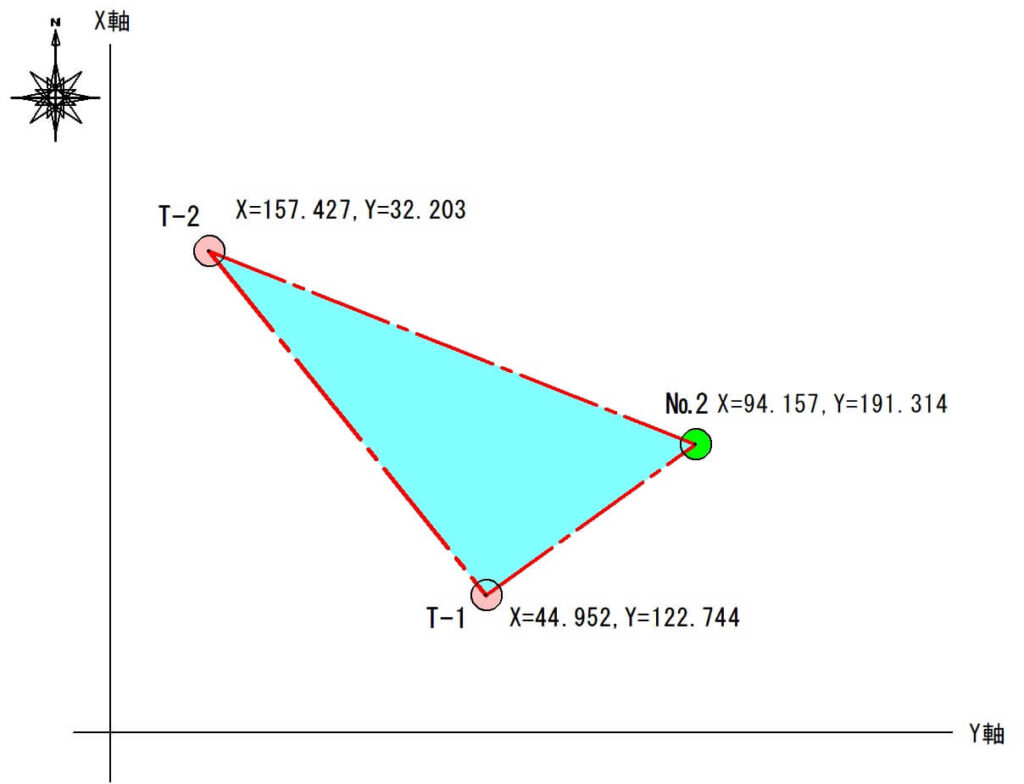
三角形(T-1、T-2、№2）の三辺を計算しよう

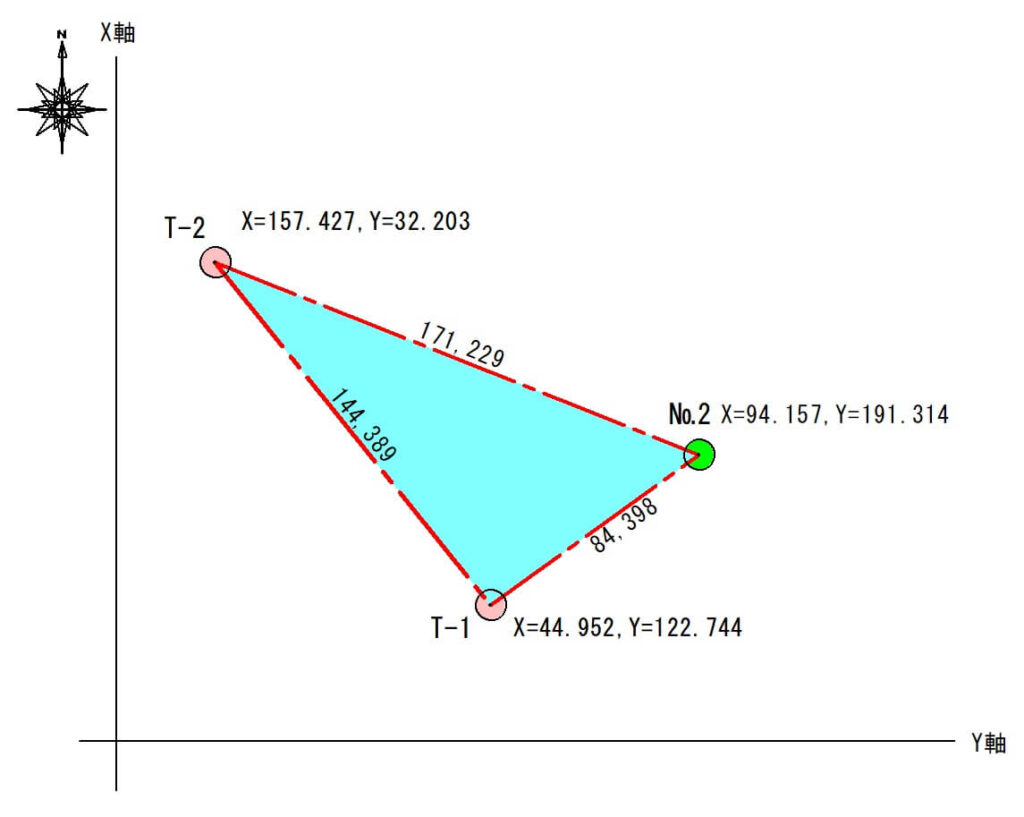
各座標点を線でつなぎ、三角形を作ります。

三角形の３辺を計算します。

T-1～T-2間の距離

T-1とT-2のX軸Y軸の差をそれぞれ計算します。

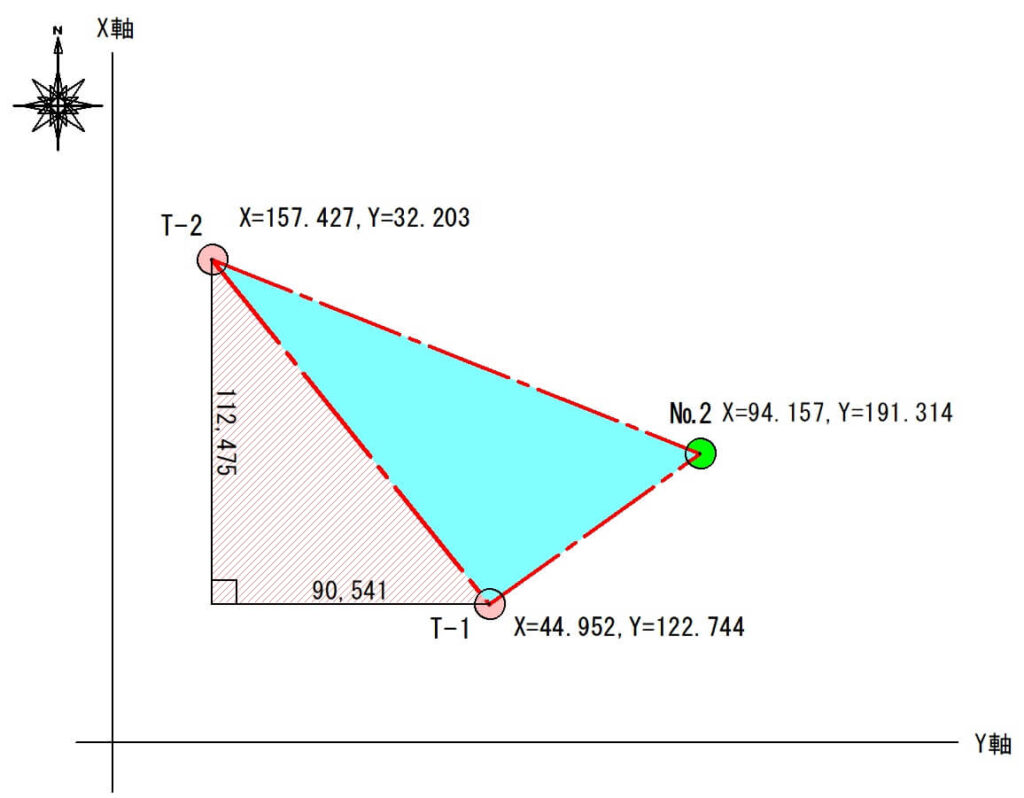
$$X軸＝157.427-44.952＝112.475ｍ$$

$$Y軸＝122.744-32.203＝90.541ｍ$$

この直角三角形から「三平方の定理」を使ってT-1～T-2間の距離を計算します。

$$T-1～T-2間の距離=\sqrt{112.475^2+90.541^2}$$

$$T-1～T-2間の距離=144.389ｍ$$

となります。

T-1～№2間の距離

次にT-1と№2のX軸Y軸の差をそれぞれ計算します。

$$X軸＝94.157-44.952＝49.205ｍ$$

$$Y軸＝191.314-122.744=68.570ｍ$$

先ほどと同じように、この直角三角形から「三平方の定理」を使ってT-1～№2間の距離を計算します。

$$T-1～№2間の距離=\sqrt{49.205^2+68.570^2}$$

$$T-1～№2間の距離=84.398ｍ$$

となります。

T-2～№2間の距離

最後にT-2と№2のX軸Y軸の差をそれぞれ計算します。

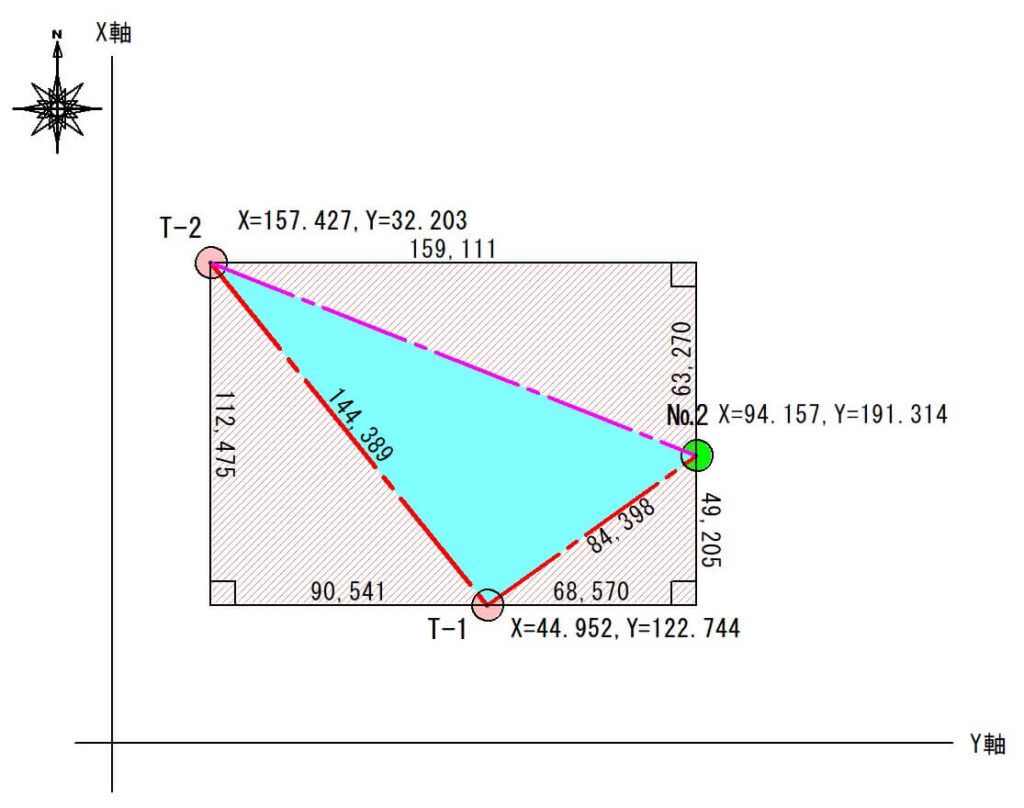
$$X軸＝157.427-94.157=63.270ｍ$$

$$Y軸＝191.314-32.203＝159.111ｍ$$

先ほどと同じように、この直角三角形から「三平方の定理」を使ってT-2～№2間の距離を計算します。

$$T-2～№2間の距離=\sqrt{63.270^2+159.111^2}$$

$$T-2～№2間の距離=171.229ｍ$$

これで、三角形(T-1、T-2、№2）の3辺の距離を計算できました。

№2までの水平角度を計算しよう

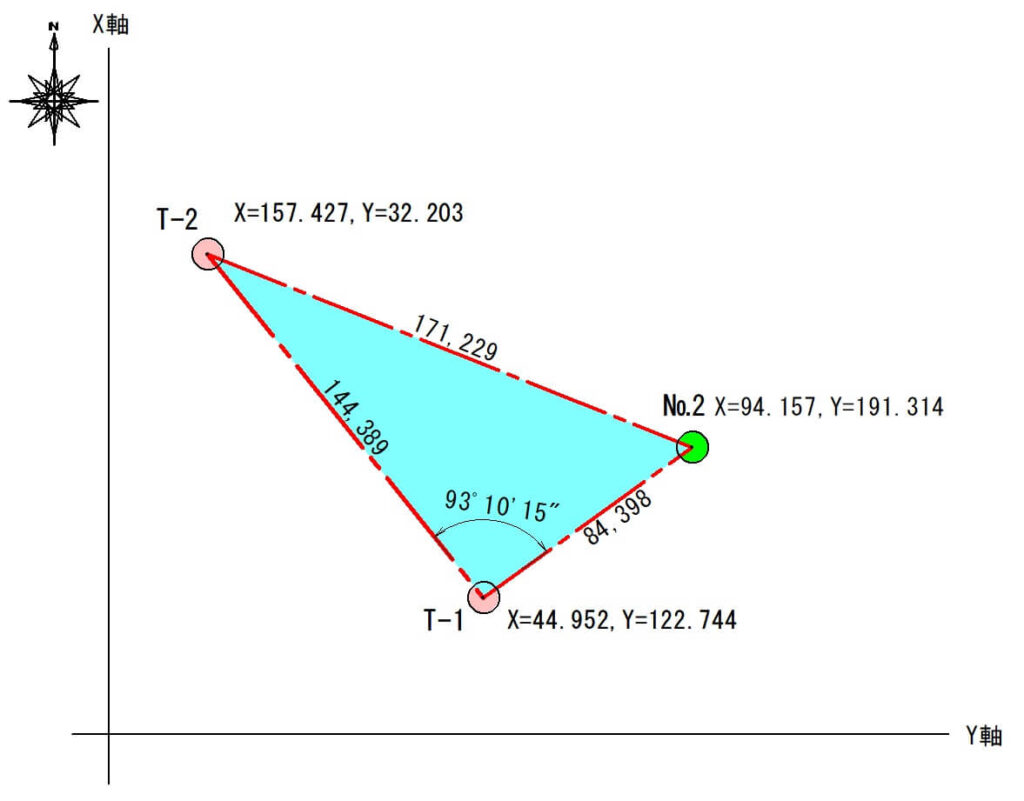
三角形(T-1、T-2、№2）の3辺の距離を計算したので、T-2を0度とした場合の「№2までの水平角度」を計算しましょう。

余弦定理を使って角度を計算します。

余弦定理の公式

$$a^2=b^2+c^2-2bc cosA$$

$$b^2=a^2+c^2-2ac cosB$$

$$c^2=a^2+b^2-2ab cosC$$

$$171.229^2=144.389^2+84.398^2-2×144.389×84.398×cosT-1$$

$$29319.370=27971.206-24372.286×cosT-1$$

$$T-1=93°10’15″$$

角度を求めるもう１つの方法「平面ベクトルの内積」

T-1の角度A【93°10′15”】を計算する方法がもう１つあります。

それが「平面ベクトルの内積」です。

これはT-1の座標点を「0.000」としてT-2と№2までのX、Y座標をもとに角度を計算します。

公式は次の通りです。

$$cosA=\frac{(X1×X2)＋(Y1×Y2)}{\sqrt{X1^2+Y1^2}×\sqrt{X2^2+Y2^2}}$$

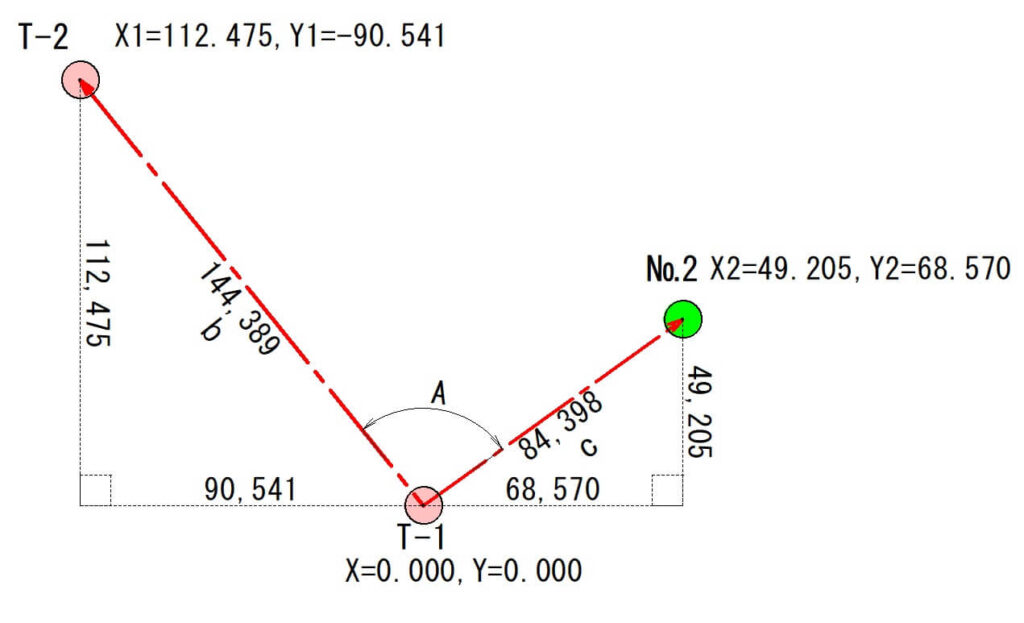
こちらの図をもとに、数値を入力して計算します。

X1、Y1は左側の三角形になります。X1＝112.475、Y1＝－90.541です。

X2、Y2は右側の三角形になります。X2＝49.205、Y2＝68.570です。

この数値を公式に入れて角度A＝93°10′15”を計算してみましょう。

$$cosA=\frac{(112.475×49.205)＋(-90.541×68.570)}{\sqrt{112.475^2+-90.541^2}×\sqrt{49.205^2+68.570^2}}$$

$$cosA=\frac{5534.332＋-6208.396}{144.389×84.398}$$

$$cosA=\frac{-674.064}{12186.143}$$

cosA=-0.05531（アークコサインで計算）

A=93.17064757°となります。

１０進法から６０進法へ変換すると93°10′14”（四捨五入の関係で1″ずれました）となります。

計算結果

T-1から№２までの「水平角度」と「水平距離」を計算した結果をまとめてみましょう。

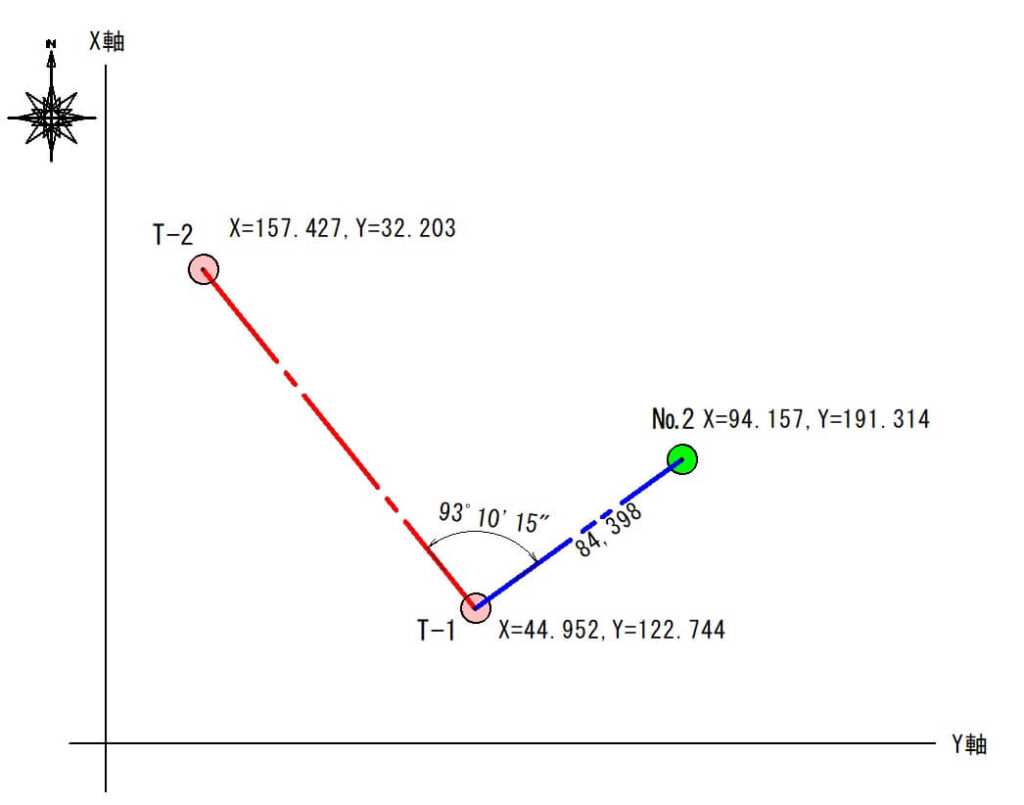
1. 既知点「T-1」にトータルステーションを据付けます。
2. 既知点「T-2」を視準し、水平角度を0セット(0°0′0″）します。
3. トータルステーションの水平角度を93°10′15″に合わせます。
4. T-1から水平距離84.398ｍの位置に№2を復旧します。

まとめ

今回のブログでは平面直角座標を使った「水平角度」と「水平距離」を計算しました。

• 3つの座標点を線で結び三角形を作ります。
• 三角形の三辺の長さを「三平方の定理」で計算します。
• 三辺の長さを使い「余弦定理」から角度を計算します。
• 角度を求めるもう1つの計算方法として「平面ベクトルの内積」を使って実際に計算しました。

以上となります。

最後までお読みいただきありがとうございました。

にほんブログ村

にほんブログ村

にほんブログ村

川下　政明

土木施工管理技士

XInstagramYouTube

川下政明（かわしもまさあき）と申します。
土木施工管理歴３０年。
地場の建設会社に勤務しております。
1級土木、2級管工事、2級舗装、測量士、採石業務管理者を保有しております。
このブログは、工事現場に関する「施工管理」・「測量」・「HO_CAD」・「JW-CAD」・「パソコン」などについて発信しています。
参考にしていただけると嬉しいです。