【後方交会法】２つの座標点から器械点座標の計算方法を解説
まさあき
建設ナビ
PR
トータルステーションの「誤差」測定距離の【精度】について
まさあき
記事内に商品プロモーションを含む場合があります
このブログでは、トータルステーションの「誤差」そして「精度」の計算方法についてわかりやすく解説させていただきます。
動画でも解説していますので、よかったら覗いてみてください。
Contents
光波測距の原理
光の変調によって作り出される波を「光波」と言います。
光波測距儀に採用されている位相差測定法は、大きな波長の光波を作り(光の変調という）２点間を往復させて戻った波と発信波との位相差を測定して距離を測定します。
下の図は位相差測定法のイメージ図です。
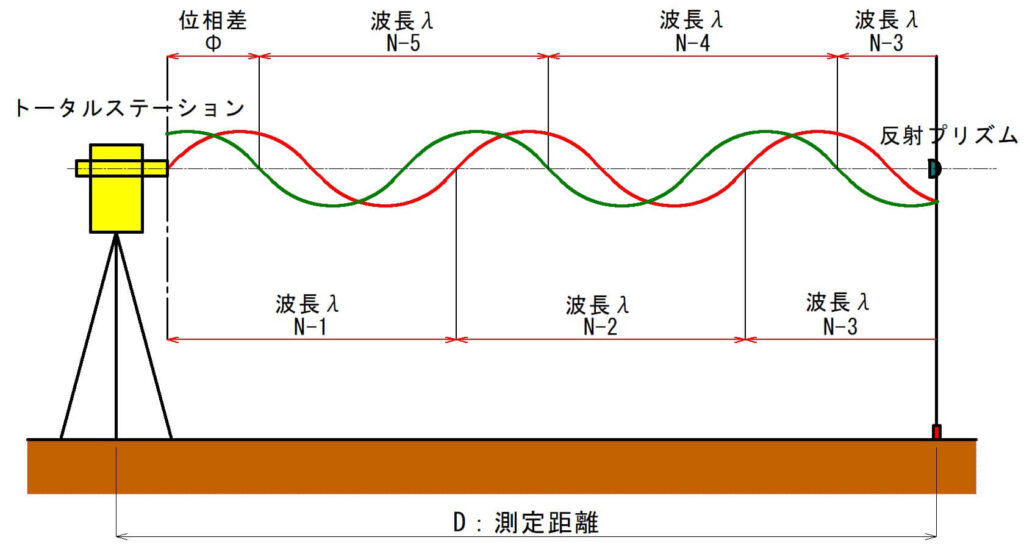
1つの波（パターン）を「波長（λ）」と呼びます。
λは「ラムダ」と呼びます。
上の図のイメージ図では、光波が反射プリズムに跳ね返り、TSに戻った時点で、波長λがN-1からN-5までで「5」あることになります。
そして、波長N-5からTSまでの端数が「位相の差（Φ）」となります。
D=(λ/2)N+{(λ/2)×(Φ-2π)}
上の数式より、波長λの数と位相差Φから測定距離（D）を算出する仕組みとなっています。
測定された測定距離（D）から鉛直角度を使用して、水平距離と高低差を算出しています。
誤差には大きく２種類あります
距離の大きさに比例して影響を与える誤差
気象要素の測定誤差
気温・気圧・湿度が、光の波に影響を与えるので、距離の大きさに比例する誤差を与えています。
変調周波数の誤差
変調周波数は、電源電圧の変化、信号発信機の老化、温度の急激な変化、衝撃等が周波数に変化を与えています。
距離の大小に無関係な誤差
位相（いそう）差の測定誤差。
光の変調によって作り出される波「波長」のずれ方をいいます。
位相差を測定する際に、どこまで小さく（1/2000で読取るか、1/1000で読み取るのか）分割して読取れるのかで、微妙な誤差が発生するというイメージです。
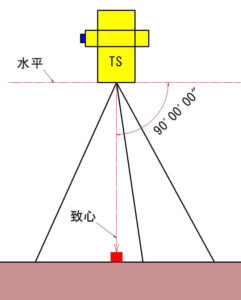
器械定数(器械の中心と光源のずれ）、反射プリズム定数（プリズム表面とピン中心までの数値のずれ）は、測定誤差がわずかに存在します。(約1～2mm）。
また、測距儀・反射プリズムの致心（ちしん）は、注意を払ったとしても２mm程度はあると考えられます。
測定距離の精度を計算してみよう
使用しているトータルステーション仕様の確認
トータルステーションの取扱説明書「仕様」の部分に【精度】が記載されています。
計算してみよう
現場では「高速連続測定」を使用しているので、
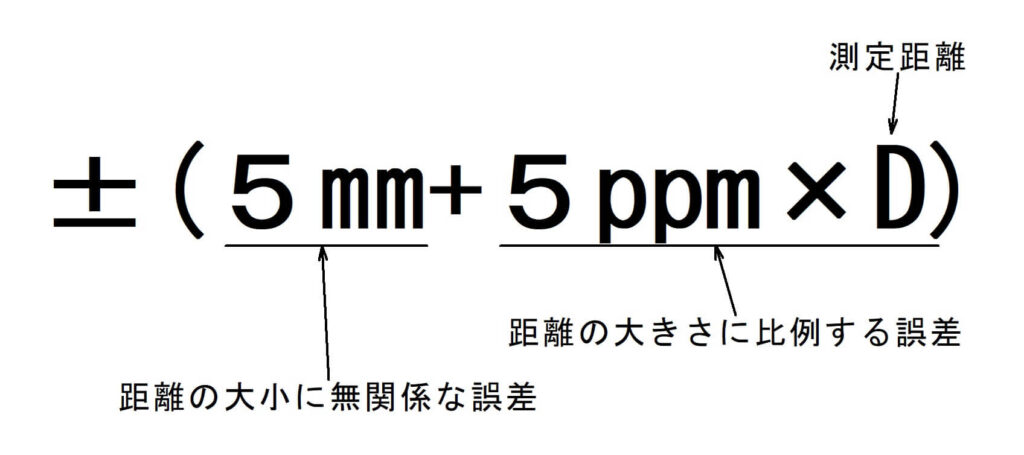
高速測定の（５㎜+５ppm×D）を計算してみます。
最初の「５㎜」は距離の大小に無関係な誤差。
次の「5PPM」は距離の大きさに比例する誤差で、百万分の1で表します。
5の百万分の一は、５ppm＝5×10-6
となります。
単位を「ｍ」に揃えて計算するとわかりやすいと思います。
測定距離を１㎞として計算してみましょう
１㎞＝1000mです。
±（0.005ｍ+0.000005×1000ｍ）＝0.010m＝10㎜
したがって、±10㎜の精度となります。
もう一つ、測定距離を100mとして計算してみましょう。
±（0.005ｍ+0.000005×100ｍ）＝0.0055m＝6㎜
したがって、±６㎜の精度となります。
公共測量トータルステーション性能区分
| 機器区分 | 測角 | 測定距離 測定角度 | 適用する測量区分 |
| トータルステーション１級 | 最小読定値 １秒読み | ２㎞を超える （５㎜+５ppm×D） | １，２級 基準点測量 |
| トータルステーション２級 | 最小読定値 １0秒読み | ２㎞を超える （５㎜+５ppm×D） | ２，３級 基準点測量 |
| トータルステーション２級 | 最小読定値 １0秒読み | ２㎞以下 （５㎜+５ppm×D） | ２，３級 基準点測量 |
| トータルステーション３級 | 最小読定値 20秒読み | ２㎞以下 （５㎜+５ppm×D） | ４級 基準点測量 |
まとめ
今回のブログでは、トータルステーションの誤差そして、測定精度の計算についてお話ししました。
最初にトータルステーションの光波測距の原理ついて解説しました。
光波測距は位相差測定法で測定距離を算出しております。
次に、測定誤差には大きく２つあるということについて解説しました。
- 距離の大きさに比例して影響を与える誤差（気象要素と変調周波数の誤差）
- 距離の大小に無関係な誤差（位相差の測定誤差と器械定数及び反射プリズム定数の誤差と、致心誤差）
測定距離の精度の計算を実際にやってみました。
お使いのトータルステーションの取扱説明書を確認してみましょう。
±（５㎜+５ppm×D）
最初の5㎜は距離の大小に無関係な誤差です。
次の5ppm×Dは距離の大きさに比例して影響を与える誤差です。
今回のブログは以上となります。
最後までお読みいただきありがとうございました。
教程 基準点測量
編著者 齋藤 博、高嶋 重雄
教程 基準点測量
 にほんブログ村 |
 にほんブログ村 |
 にほんブログ村 |
ABOUT ME
川下政明（かわしもまさあき）と申します。
土木施工管理歴３０年。
地場の建設会社に勤務しております。
1級土木、2級管工事、2級舗装、測量士、採石業務管理者を保有しております。
このブログは、工事現場に関する「施工管理」・「測量」・「HO_CAD」・「JW-CAD」・「パソコン」などについて発信しています。
参考にしていただけると嬉しいです。
土木施工管理歴３０年。
地場の建設会社に勤務しております。
1級土木、2級管工事、2級舗装、測量士、採石業務管理者を保有しております。
このブログは、工事現場に関する「施工管理」・「測量」・「HO_CAD」・「JW-CAD」・「パソコン」などについて発信しています。
参考にしていただけると嬉しいです。
