【偏角弦長法】カーブ上の測点を測量しよう

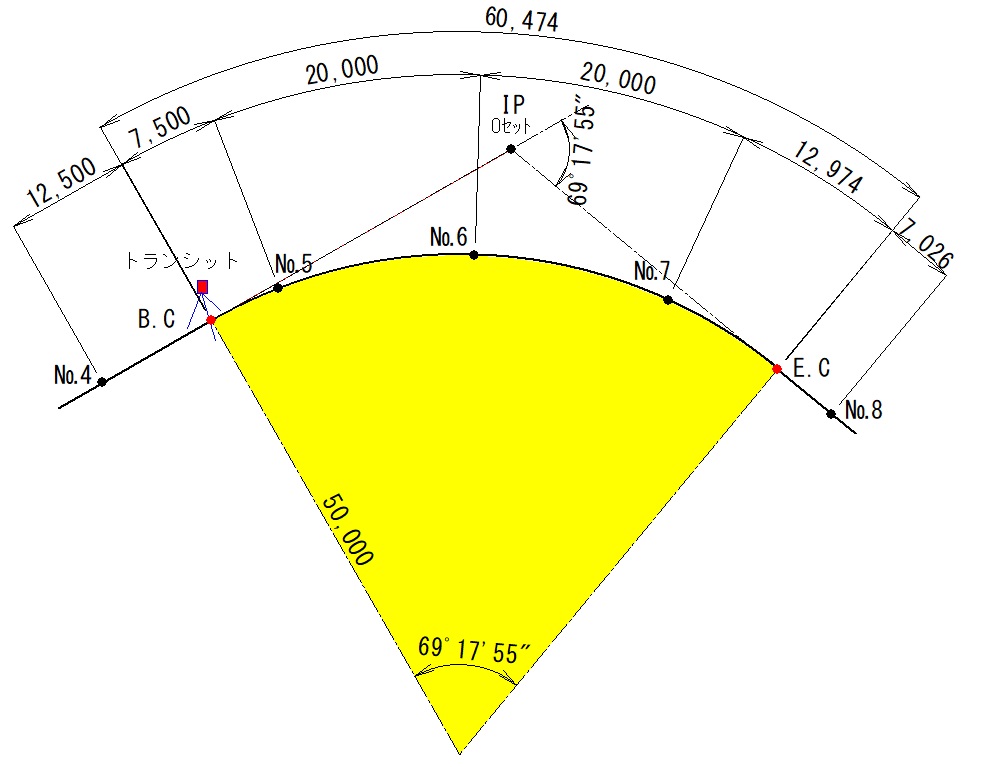
B.Cにトランシットを据えて、接線方向からの偏角δ（デルタ）と距離(弦長c)により、曲線上の中間点(測点)を求めていく方法です。

計算公式

B.Cにトータルステーションを据付けてI,Pを視準し０°セットした状態で角度を計算します。

偏角（角度）と距離（弦長）の計算式は次の通りです。

• R:曲線半径(radius of curve)
• cl：曲線長(curve length)

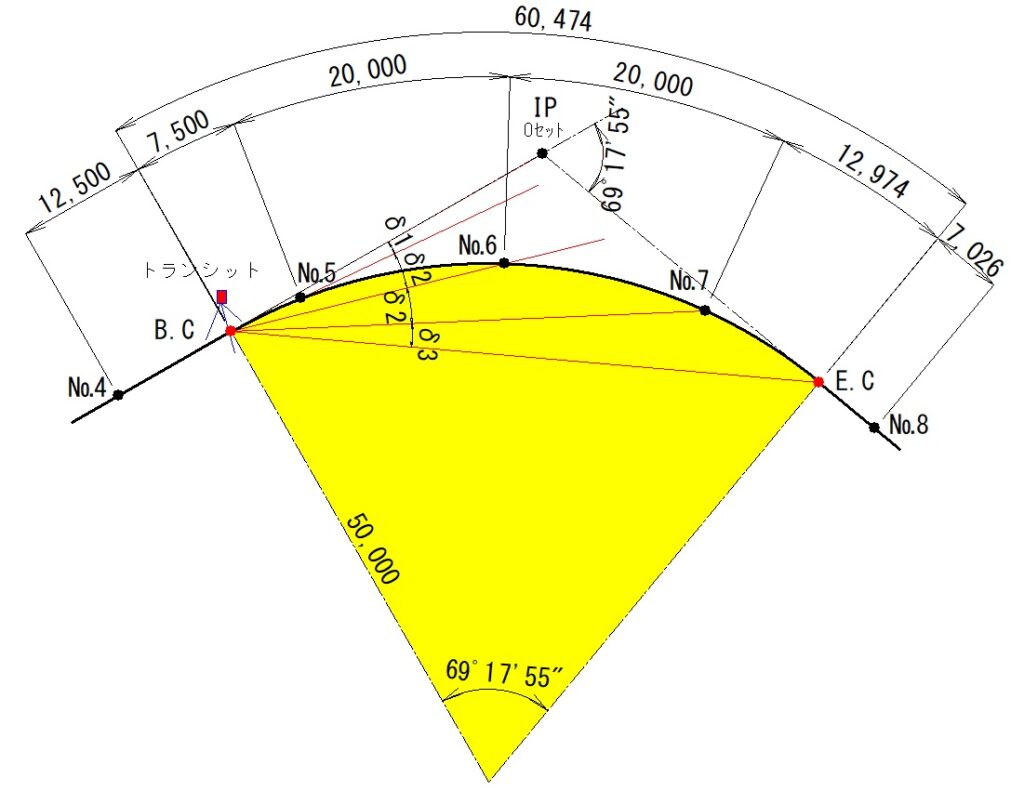
偏角δを計算して見よう

cl（曲線長）は「7.500ｍ」、「20.000ｍ」、「12.974ｍ」の３種類です。

• δ1＝1718.87×7.50÷50.0＝257.8305分＝4°17′49.83″
• δ2＝1718.87×20.0÷50.0＝687.548分＝11°27′32.88″
• δ3＝1718.87×12.974÷50.0＝446.01分＝7°26′0.74″

δ1、δ2、δ3の計算結果を使って、№5、№6、№7，E,Cまでの角度を計算します。

• №5＝δ1＝4°17′49.83″
• №6＝δ1＋δ2＝4°17′49.83″＋11°27′32.88″＝15°45′22.71″
• №7＝δ1＋δ2＋δ2＝15°45′22.71″＋11°27′32.88″＝27°12′55.59″
• EC＝δ1＋δ2＋δ2+δ3＝27°12′55.59″+7°26′0.74″＝34°38′56.33″

ECまでの角度は中心角69°17′55″の１/2となるので確認してみます。

I／2＝69°17′55″÷2＝34°38′57.5″

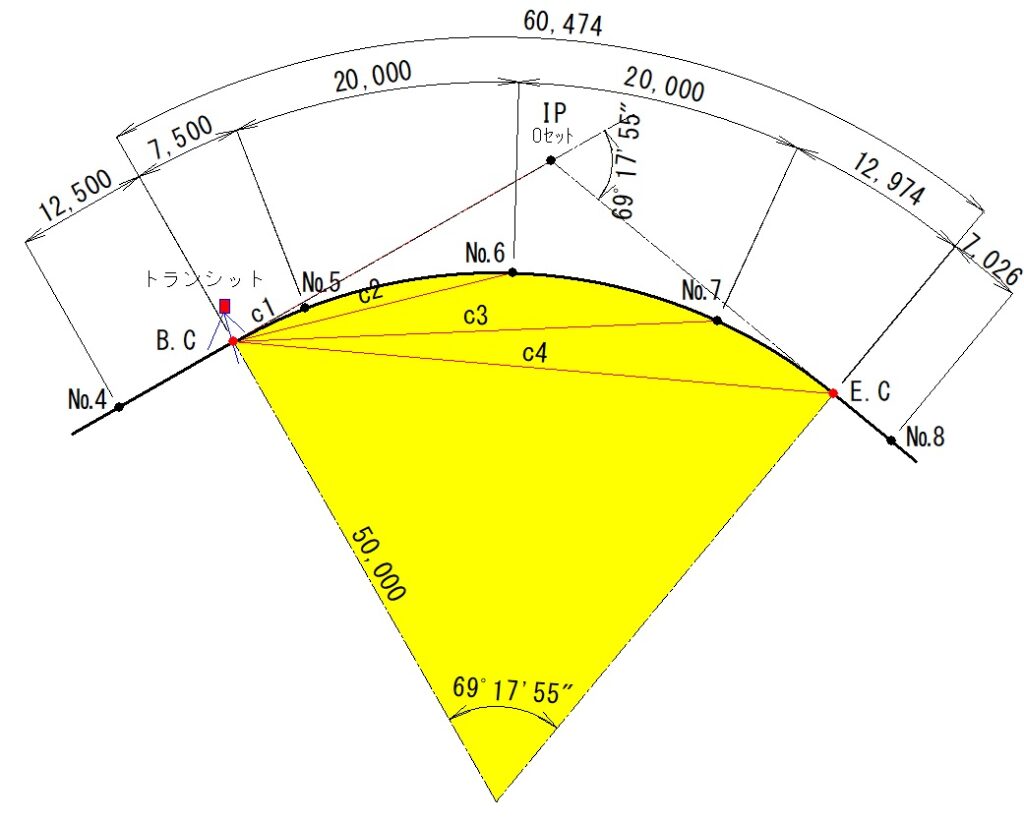
弦長cを計算して見よう

BCから各測点までの弦長c（水平距離）を計算します。

• c1=2×50.0×sin4°17′49.83″＝7.493m
• c2=2×50.0×sin15°45′22.71″＝27.155m
• c3=2×50.0×sin27°12′55.59″＝45.734m
• c4=2×50.0×sin34°38′56.33″＝56.855m

カシオ　CASIO　プログラム関数電卓　fx-72F

created by Rinker

¥4,530 (2025/04/02 02:49:12時点 楽天市場調べ-詳細)

• Amazon
• 楽天市場
• Yahooショッピング
• メルカリ

おわりに

今回のブログでは、B.Cにトランシットを据えてIP接線方向を０°としての、偏角δ（デルタ）と曲線上の中間点(測点)までの距離(弦長c)の計算方法を解説させていただきました。

計算結果は次のようになります。

• №5＝4°17′49.83″　c1=7.493m
• №6＝15°45′22.71″　c2=27.155m
• №7＝27°12′55.59″　c3=45.734m
• EC＝34°38′56.33″　c4=56.855m

以上となります。

最後までお読みいただきありがとうございました。

エース 測量学 （エース土木工学シリーズ） [ 福本 武明 ]

created by Rinker

¥4,290 (2025/04/01 21:11:16時点 楽天市場調べ-詳細)

• Amazon
• 楽天市場
• Yahooショッピング
• メルカリ

にほんブログ村

にほんブログ村

にほんブログ村

川下　政明

土木施工管理技士

XInstagramYouTube

川下政明（かわしもまさあき）です。
土木施工管理歴３０年以上のベテラン施工管理技士として、現場のリアルを発信中！
■施工管理のノウハウ
■測量のコツ・CADの活用法
■パソコンを使った業務効率化
【保有資格】
・1級土木施工管理技士
・2級管工事施工管理技士
・2級舗装施工管理技士
・測量士
・採石業務管理者など
建設現場で役立つ情報を「わかりやすく」「実践的に」お届けします！
仕事のヒントにしていただけると嬉しいです。