単曲線【単カーブ】の記号・名称・公式について解説します
まさあき
建設ナビ
PR
【座標「X,Y」】について解説します｜座標は位置を表す点（現場測量）
まさあき
記事内に商品プロモーションを含む場合があります
このブログは、測量で使用する「X,Y座標」についてわかりやすく解説したブログとなります。
Contents
座標
座標とは、「点（ポイント）」の位置を指定するための数値で、地球上のどの位置なのかを数値で表しています。
この座標の数値は測量、地図作成、土地の管理、大規模土木工事などの基準となります。
小規模工事の場合、現場独自の座標を組む場合もあります。
座標は地球上の位置を表す
実際の地球は赤道方向に長い回転楕円体の形をしています。
この地球上の点の位置の表し方に2つの方法があります。
- 球体と考えた場合の緯度経度による方法
- 平面と考えた場合の平面直角座標法（測地座標法）
緯度経度による方法
地球の広い範囲について考える場合に用いられます。
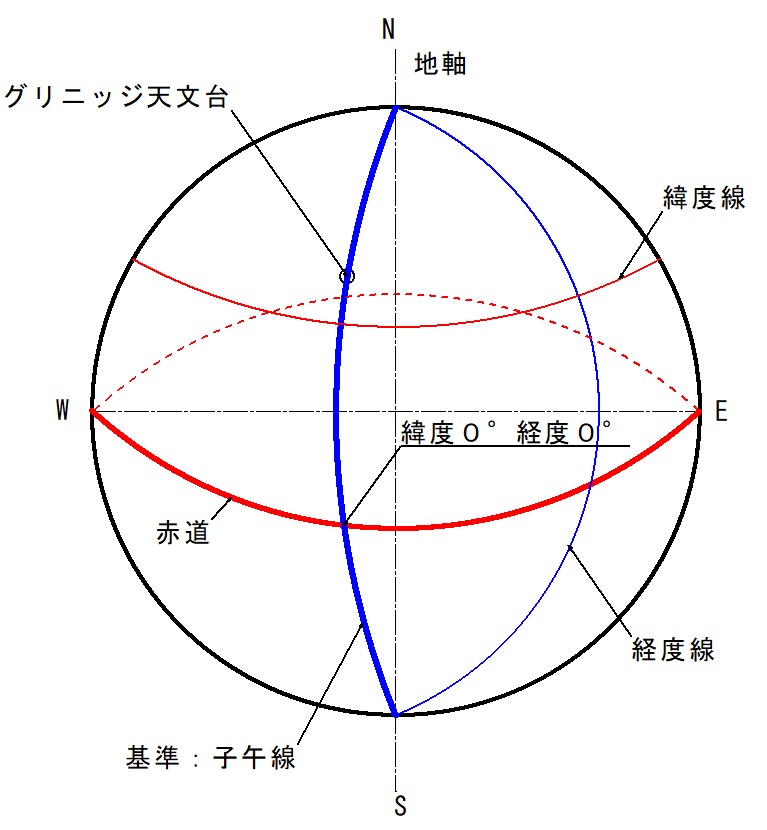
- 緯度：赤道を基準とします。北緯９０度までと南緯９０度まで。
- 経度：イギリスのグリニッジ天文台を０度とします。東経１８０度までと西経１８０度まで。
平面直角座標
通称「公共座標」とも言われています。この座標は基本測量、公共測量のみならずほとんどの測量に用いられています。
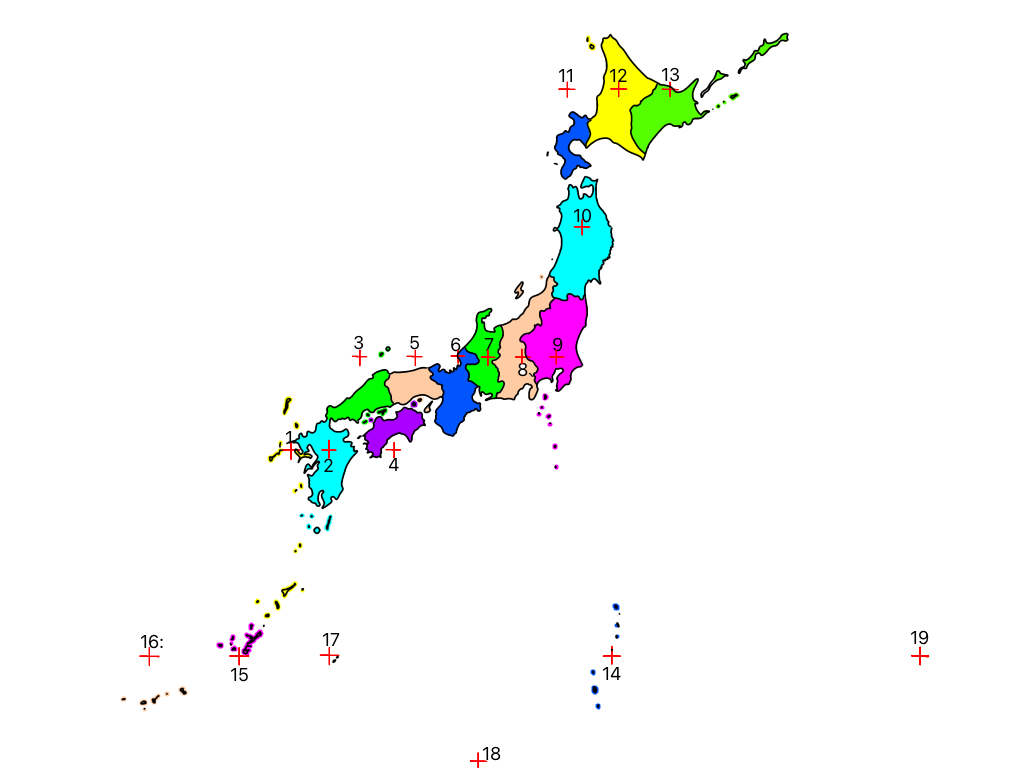
- 全国を19の座標系に分け、距離のひずみが1/10000以上にならないように東西範囲を設定しています。https://www.gsi.go.jp/sokuchikijun/jpc.html
- 座標系の境界は経緯度ではなく県境に設定されています。
ローカライゼーション
GNSSの計測座標（球体）を平面直角座標に変換します。
ICT施工の際にX,Y座標の他に標高も必要となります。
例として座標と座標の距離を計算してみよう
例として座標計算の基本的な考え方を図を使ってお話しします。
下の図は、2つの点（ポイント）を座標で表したものです。
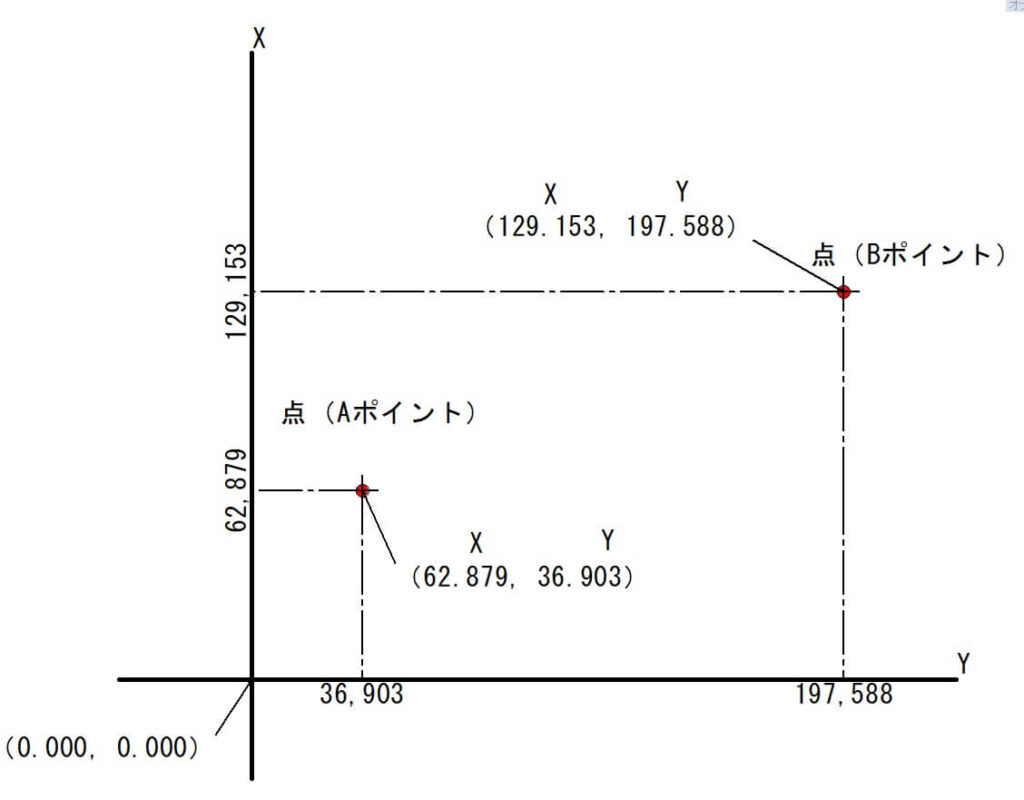
左下の点の座標が（X,Y）＝（62.879，36.903）
つまり、縦軸方向に62.879ｍ進み、横軸方向に36.903ｍ進んだポイントです。
右上の点の座標が（X,Y）＝（129.153，197.588）
縦軸方向に129.153ｍ進み、横軸方向に197.588ｍ進んだポイントです。
この2つの座標の間の距離を計算してみましょう。
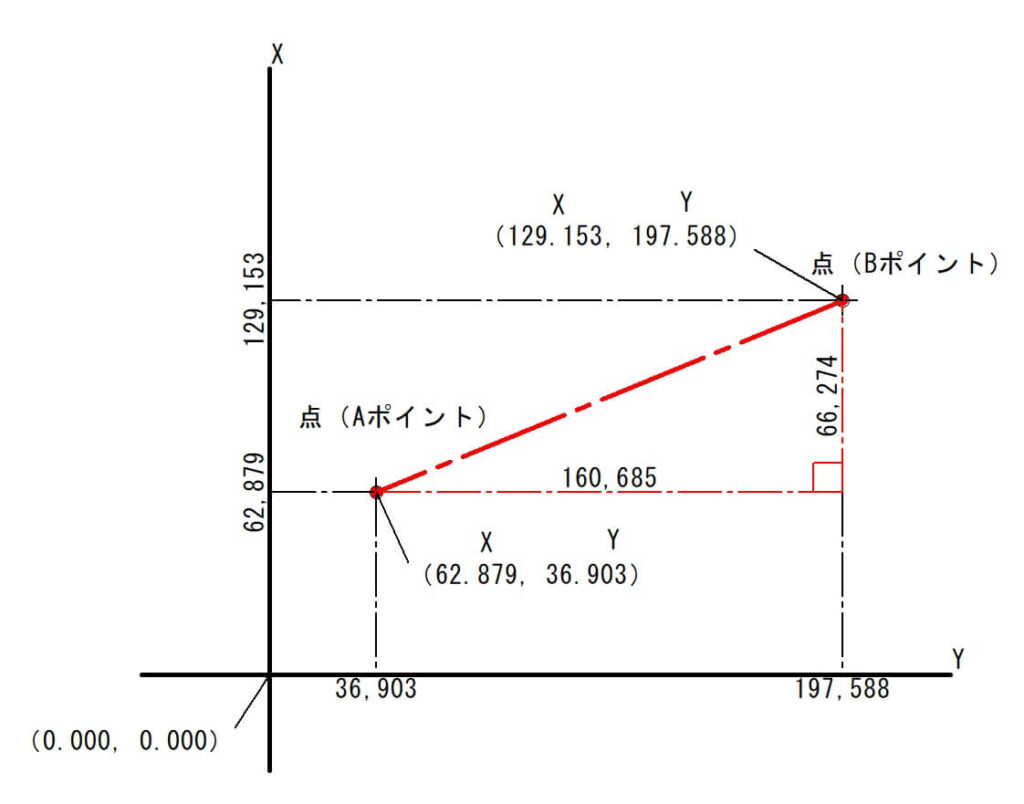
最初に「X」座標の差を計算します。
２つの点のXとXを引き算します。
$$129.153-62.879＝66.274m$$
次に「Y」座標の差を計算します。
Xと同じようにYとYを引き算します。
$$197.588-36.903＝160.685ｍ$$
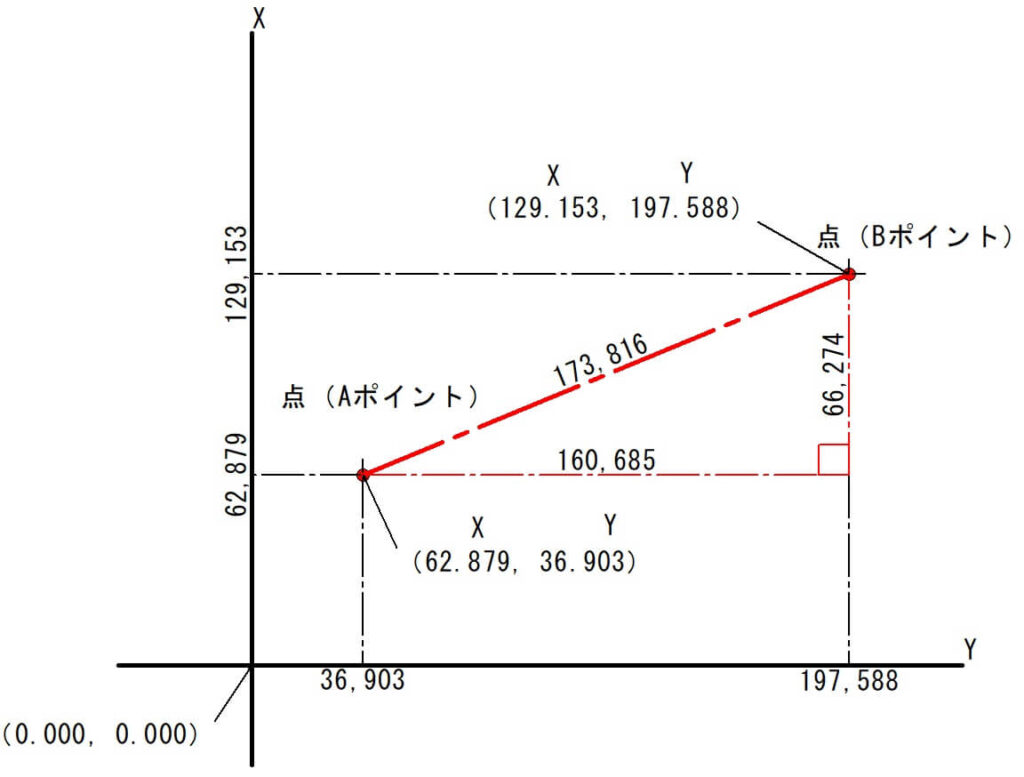
この直角三角形の斜辺を三平方の定理で計算すると「座標間の距離」を求めることができます。
$$a^2=x^2+y^2$$
$$a=\sqrt{66.274^2+160.685^2}$$
$$a=173.816$$
したがって、座標間の距離は「173.816ｍ」となります。
座標データのやり取りについて
SIMAデータについて
座標データのやり取りは「SIMAデータ」で行うことがほとんどです。
SIMA(シーマ)データーとは
測量の座標値を管理する目的で日本測量機器工業会が策定しているフォーマットです。
SIMAデーターはテキストファイルです。
拡張子は.sim。
これは「HO_CAD pao」でSIMAデータを読み込んだものになります。
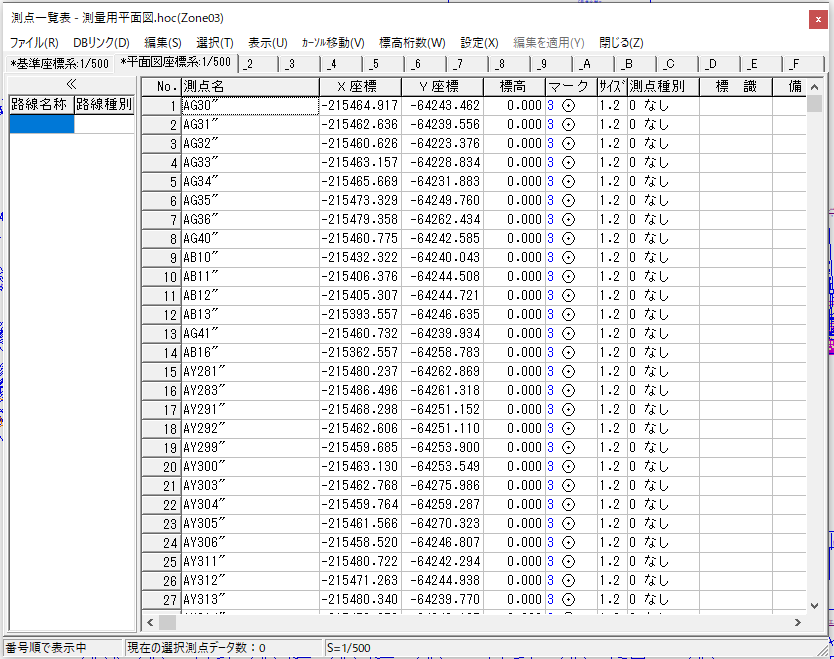
CSVデータについて
CSVデータとは、各項目がカンマ（,）で区切られたテキストデータのことで、互換性が高く、ほとんどのソフトに取り込んで閲覧、編集することが可能です。拡張子は「.csv」となります。
ウェイポイントについて
ちなみにですが、「ウェイポイント」という点もあります。
ウェイポイントは、航路設定の目印になる点で、航路の計画や追跡に利用されています。例えば、パイロットや船員は、目的地や経由地へ向かうルートを計画する際にウェイポイントを利用します。
ウェイポイントにはアルファベット５文字で名前をつけるという世界的なルールがあります。日本国内には面白いご当地WPが多数あります。
「MIKAN（みかん）」、「POTET（ポテト）」、「ONIKU（お肉）」、「KIRIN（キリンビール）」、「MALTS（モルツ）」、「EDOJO（江戸城）」など。
あわせて読みたい
平面図上に【測量系座標】を表示させたり、読取ったりする機能があります｜HO_CAD pao
あわせて読みたい
【後方交会法】２つの座標点から器械点座標の計算方法を解説
終わりに
今回のブログでは「座標」についてわかりやすく解説させていただきました。
- 座標とは、「点（ポイント）」の位置を指定するための数値で、地球上のどの位置なのかを数値で表しています。
- X軸が縦でY軸が横となり、小中学校で学習したものと逆になっています。
- 角度の測り方も逆です。
- 座標間の距離を計算するには、X座標同士の差とY座標同士の差を「三平方の定理」で求めます。
- 座標は「SIMA」や「CSV」のテキストファイルとしてやり取りされます。
以上、最後まで読んでいただきありがとうございました。
皆様のスキルアップにつながれば幸いです。
参考
「絵とき測量(改訂２版）」オーム社、粟津清蔵監修、包国勝・茶畑洋介・平田健一・小松博英 共著
「三訂 教程 基準点測量」山海堂、斉藤博・高嶋重雄 著
 にほんブログ村 |
 にほんブログ村 |
 にほんブログ村 |
ABOUT ME
川下政明（かわしもまさあき）と申します。
土木施工管理歴３０年。
地場の建設会社に勤務しております。
1級土木、2級管工事、2級舗装、測量士、採石業務管理者を保有しております。
このブログは、工事現場に関する「施工管理」・「測量」・「HO_CAD」・「JW-CAD」・「パソコン」などについて発信しています。
参考にしていただけると嬉しいです。
土木施工管理歴３０年。
地場の建設会社に勤務しております。
1級土木、2級管工事、2級舗装、測量士、採石業務管理者を保有しております。
このブログは、工事現場に関する「施工管理」・「測量」・「HO_CAD」・「JW-CAD」・「パソコン」などについて発信しています。
参考にしていただけると嬉しいです。
