座標を計算しよう｜角度と距離から計算する現場測量

今回のブログでは、関数電卓を使った平面直角座標の計算方法について説明します。

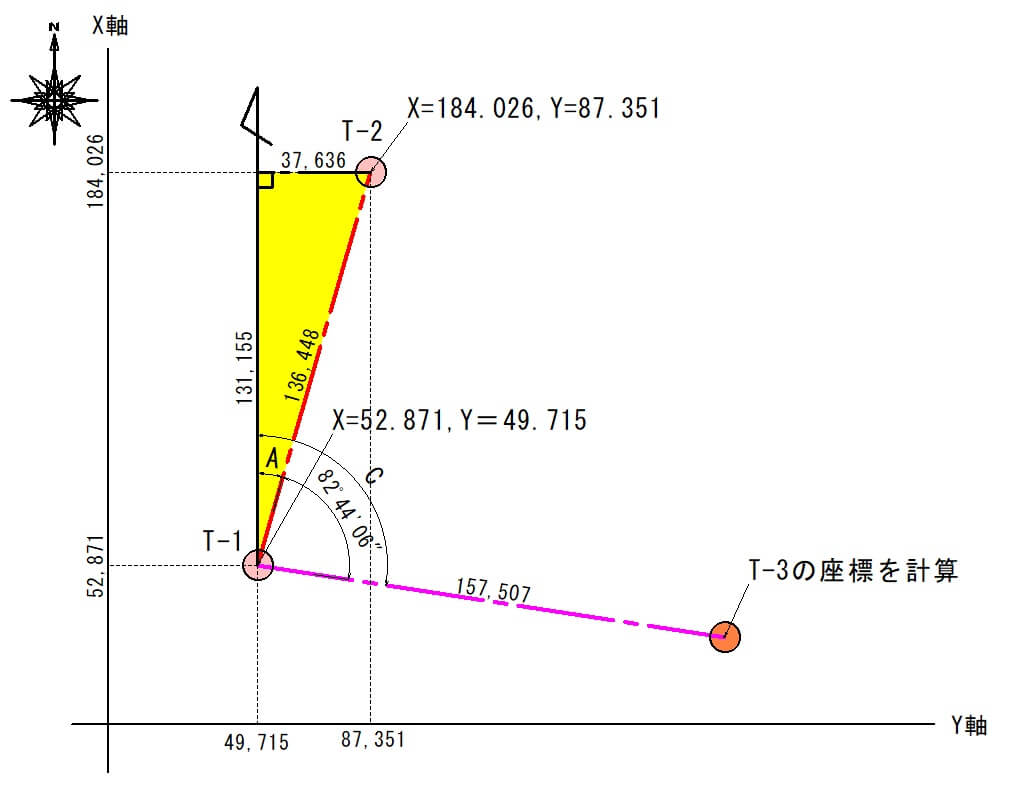
例として下の図のような状況を設定しましたので、「T-3」の座標値を計算してみましょう。

あわせて読みたい

【XY座標軸と角度】測量と算数での考え方の違い

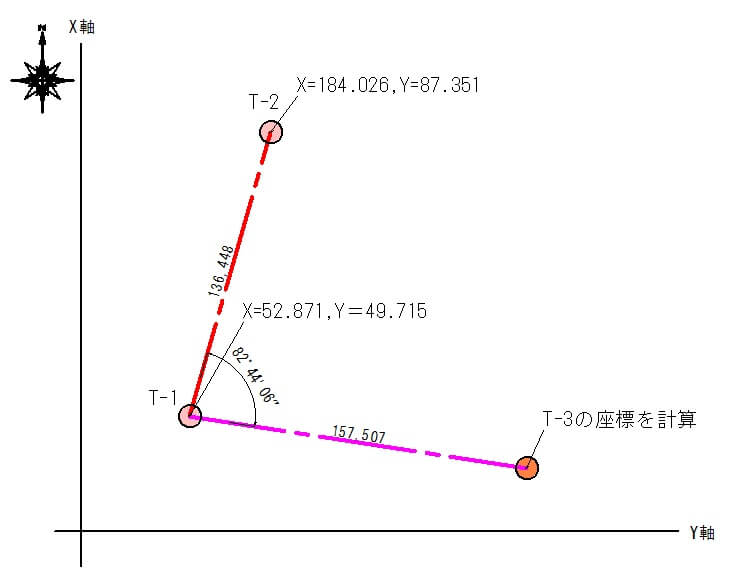
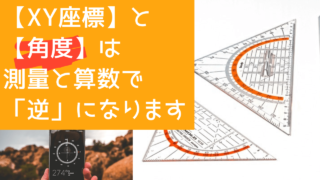
この図の状況は次の通りです。

1. トータルステーションを既知点「T-1」に据えて「器械点」とします。
   T-1の平面直角座標（X=52.871,Y＝49.715）
2. 次に「後視点」として既知点「T-2」を視準し、水平角度を0度（０°0′0″）にセットします。
   T-2の平面直角座標（X=184.026,Y=87.351）
3. 最後に、座標を求めたいポイント「T-3」を視準し、水平角度と水平距離を測ります。
   測量した結果です。
   水平角度＝82°44′06″
   水平距離＝157.507m

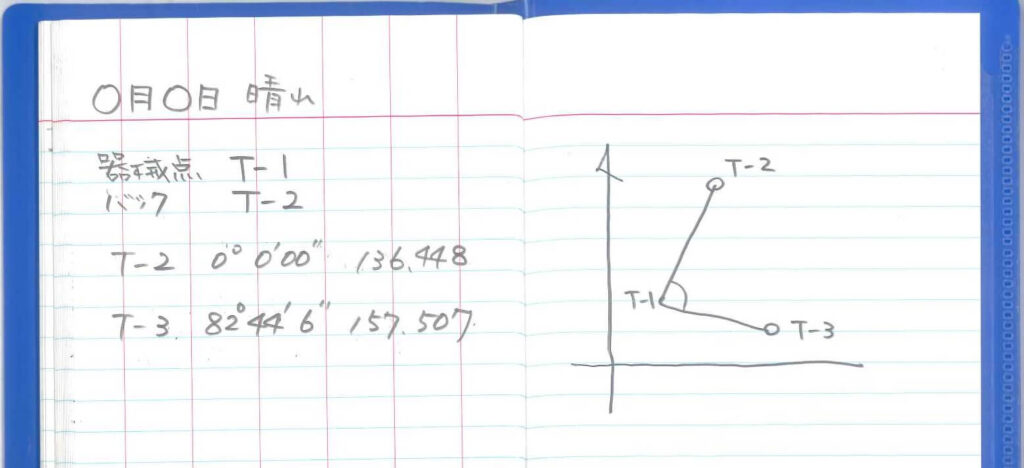
手計算で座標を計算する場合は、レベルブックに大まかな座標の位置関係を略図として記入し確認しておきましょう。

方向角Aの計算

T-1～T-2を視準した線(136.448m)の方向角「A」を計算しましょう。

T-1の座標値とT-2の座標値の「X軸」と「Y軸」の差をそれぞれ計算して直角三角形を作ります。

X軸の差＝52.871-184.026＝-131.155ｍ

Y軸の差＝49.715-87.351＝37.636m

この直角三角形を使い、Aの角度を三角関数を使って計算します。

$$tanA=\frac{37.636}{131.155}$$

tanA=37.636÷131.155=16.01126522°（アークタンジェント）

10進法から60進法へ変換すると16°0′40″となります。

ということで、方向角Aは「16°0′40″」となります。

角度Bの計算

方向角Aと測量した水平角度82°44′06″を180°から引いて角度「B」を計算しましょう。

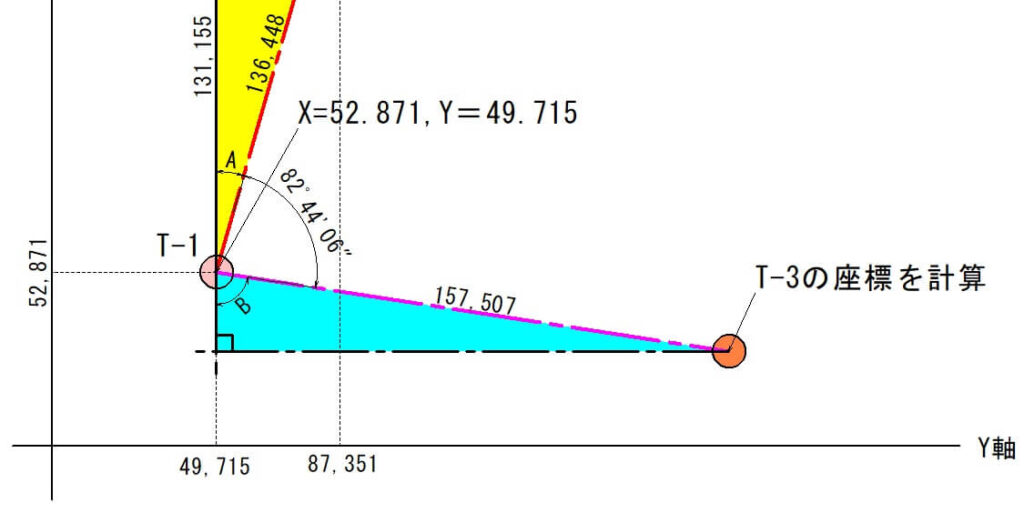
角度B＝180°-（16°0′40″+82°44′06″）＝81°15′14″

ということで、角度Bは「81°15′14″」となります。

T-1からT-3のx,y軸の差

T-1からT-3までの「X軸」と「Y軸」の差を三角関数を使って計算します。

$$cos81°15′14″=\frac{X軸の差}{157.507}$$

X軸の差＝cos81°15′14″×157.507＝23.950

$$sin81°15′14″=\frac{Y軸の差}{157.507}$$

Y軸の差＝sin81°15′14″×157.507＝155.675

ということで、
X軸の差＝23.950m
Y軸の差＝155.675m
となります。

T-3の座標値

T-1の座標値に先ほど計算したT-3までのX軸Y軸の差を加えましょう。

X軸はT-1から見て「下向き」なのでマイナス、
Y軸はT-1から見て「右向き」なのでプラスとなります。

T-3のX軸＝T-1のX軸52.871-23.950＝28.921

T-3のY軸＝T-1のY軸49.715+155.675＝205.390

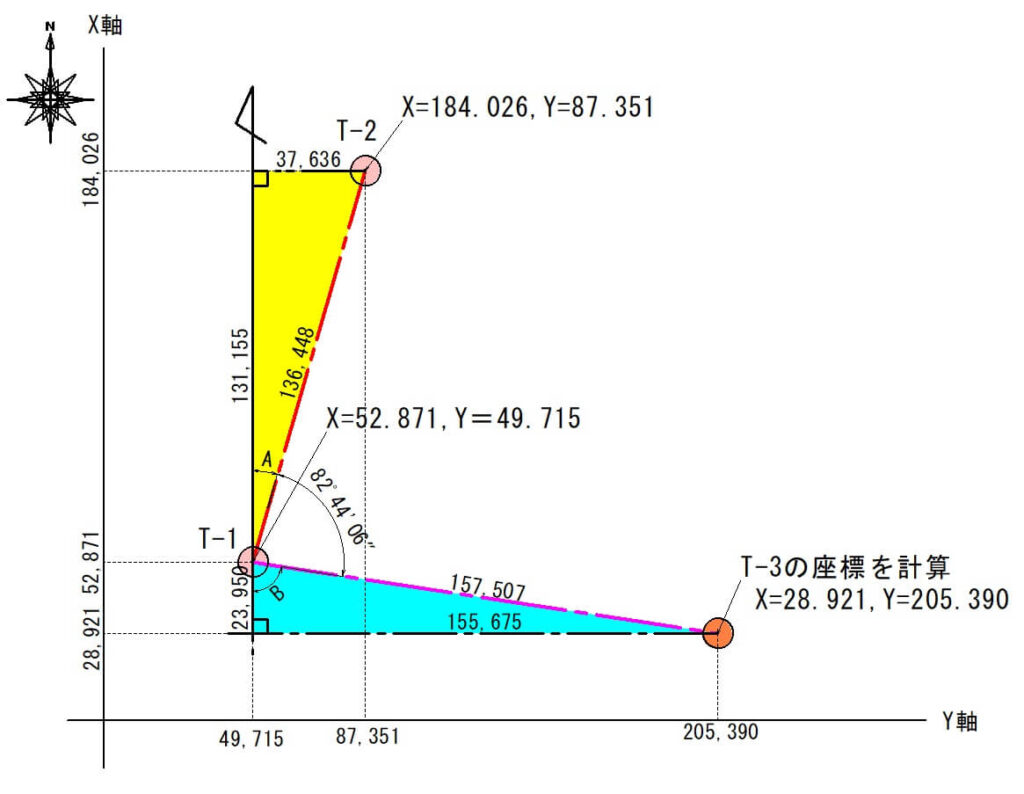
ということで、「T-3」の座標値の計算結果

X＝28.921ｍ
Y＝205.390m

となります。

方向角Cからの計算

角度Bから三角関数を使ってX軸の差とY軸の差を計算しましたが、方向角Cから直接計算することができます。

線T-1～T-3（ピンク色の線）の方向角Cを計算します。

方向角C＝方向角A＋測量した角度＝16°0′40″+82°44′06″＝98°44′46″

となります。

方向角Cを使って、三角関数でX軸の差とY軸の差を計算します。

計算方法の考え方は、水色の直角三角形と同じになります。

$$cos98°44′46″=\frac{X軸の差}{157.507}$$

cos98°44′46″×157.507＝－23.950

$$sin98°44′46″=\frac{Y軸の差}{157.507}$$

sin98°44′46″×157.507＝155.675

計算結果を「T-1」の座標に加えるとT-3の座標を計算できます。

慣れてくるとこちらの計算が早いのですが、最初のうちは直角三角形を作りながらの計算がおすすめです。

まとめ

今回のブログは、平面直角座標の計算方法を１つの例を使って解説させていただきました。

1. 座標点の位置関係を略図を作成して確認します。
2. 器械点と後視点の座標値の差（X軸・Y軸）を計算します。
3. 計算した座標値の差を使って「方向角」を計算します。
4. 方向角を利用して、計算したい点「T-3」までの座標値の差（X軸・Y軸）を計算します。
5. 基準と下器械点「T-1」に座標値の差を加えて「T-3」の座標値を計算します。

計算方法のポイントは「略図」を作図し、座標の位置関係を確認しておくことと、「方向角の計算」です。

以上となります。

最後までお読みいただきありがとうございました。

にほんブログ村

にほんブログ村

にほんブログ村

川下　政明

土木施工管理技士

XInstagramYouTube

川下政明（かわしもまさあき）と申します。
土木施工管理歴３０年。
地場の建設会社に勤務しております。
1級土木、2級管工事、2級舗装、測量士、採石業務管理者を保有しております。
このブログは、工事現場に関する「施工管理」・「測量」・「HO_CAD」・「JW-CAD」・「パソコン」などについて発信しています。
参考にしていただけると嬉しいです。