【土方カーブ】を計算しよう！

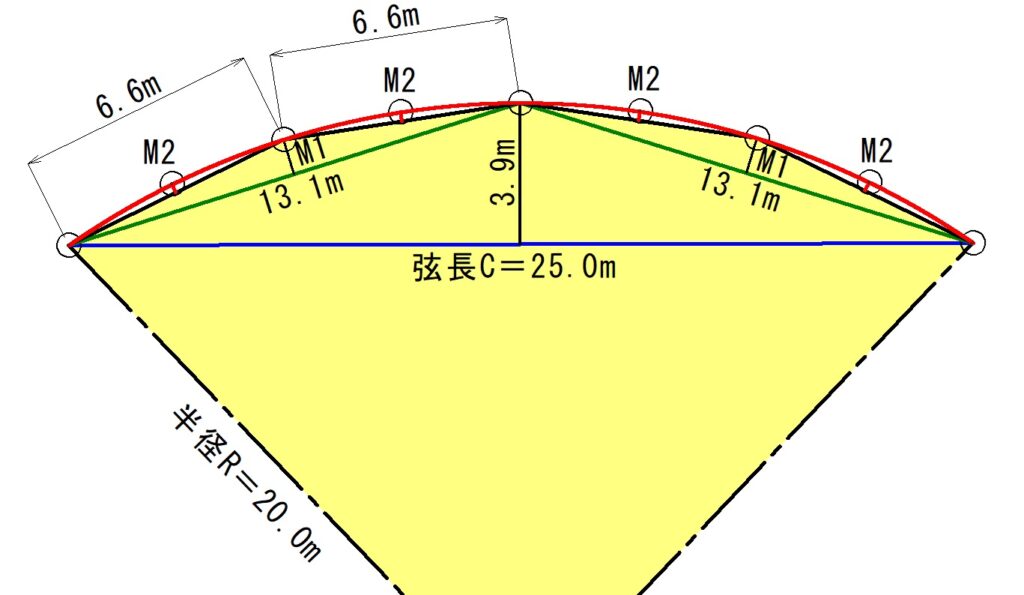
「土方カーブ」は、下の図の【M、M1、M2～】の長さ（中央縦距）を計算して現地に曲線の法線を点で設置していきます。

土方カーブは、中央縦距法・1/4法とも呼ばれています。

中央縦距Mの公式

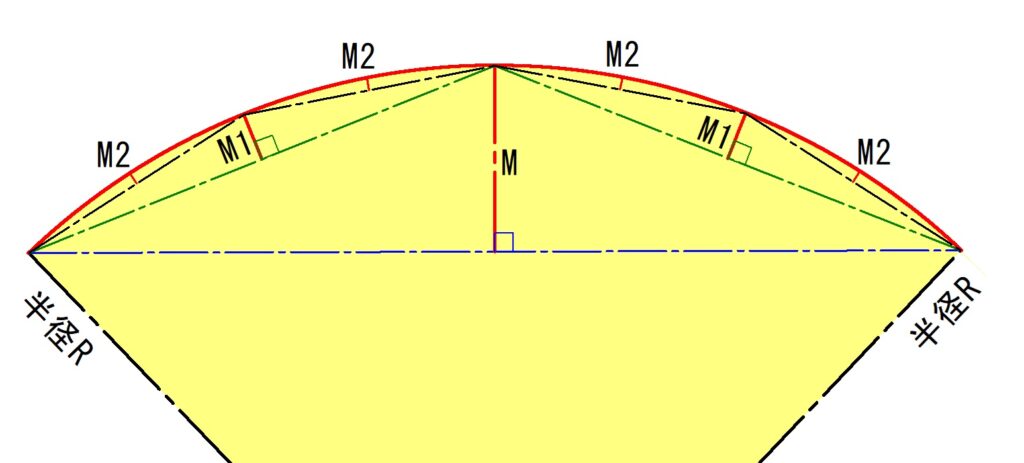
$$M=\frac{C^2}{8R}$$

$$M1=\frac{M}{4}$$

$$M2=\frac{M1}{4}$$

【C】＝弦長（青い直線、緑の直線）
【R】＝曲線半径

Mを計算しよう

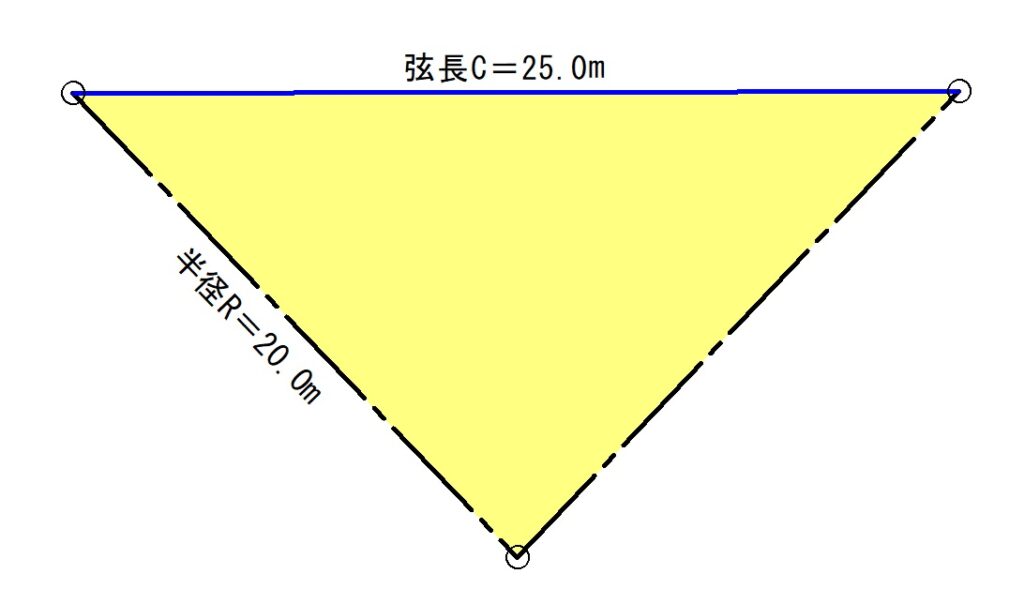
曲線半径R＝20.0m、弦長C＝25.0mとして土方カーブを計算しましょう。

弦長Cの中間点でオフセットを立てて中央縦距【M】を計算します。

$$M=\frac{25.0^2}{8×20.0}$$

$$M≒3.9ｍ$$

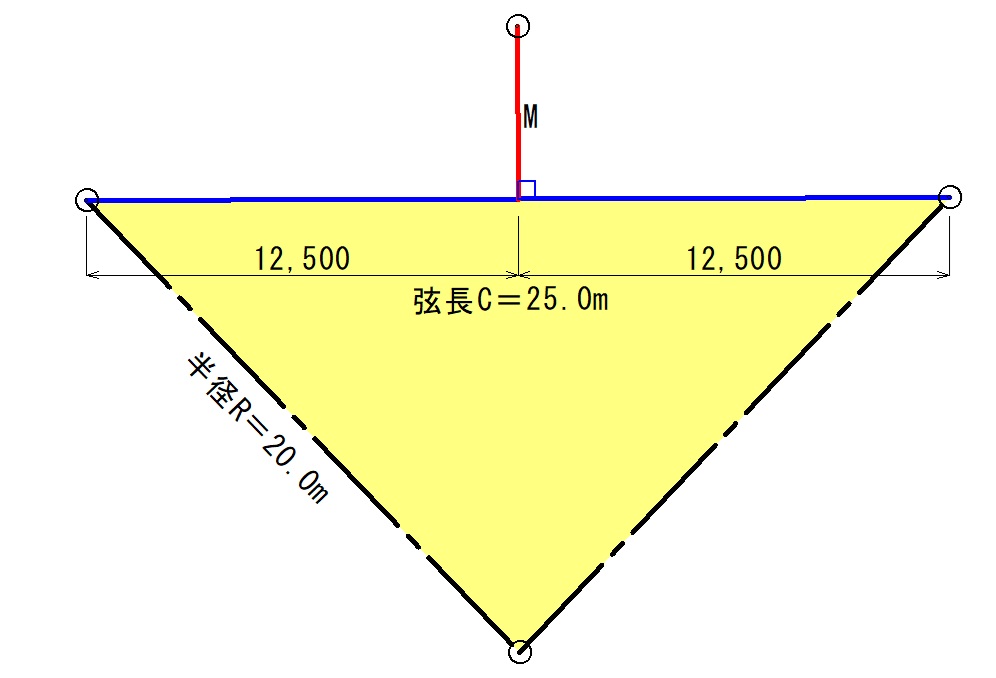
中央縦距【M】は3.9ｍとなります。

次に、中央縦距Mの頂点からの弦長を引いて距離13.1mを測ります。

弦長13.1mの中間点でオフセットを立てて中央縦距【M1】を計算します。

$$M1=\frac{3.9}{4}$$

$$M1≒1ｍ$$

中央縦距【M1】は1.0ｍとなります。

次に、中央縦距Mの頂点からの弦長を引いて距離6.6mを測ります。

弦長6.6mの中間点でオフセットを立てて中央縦距【M2】を計算します。

$$M2=\frac{1.0}{4}$$

$$M2≒0.3ｍ$$

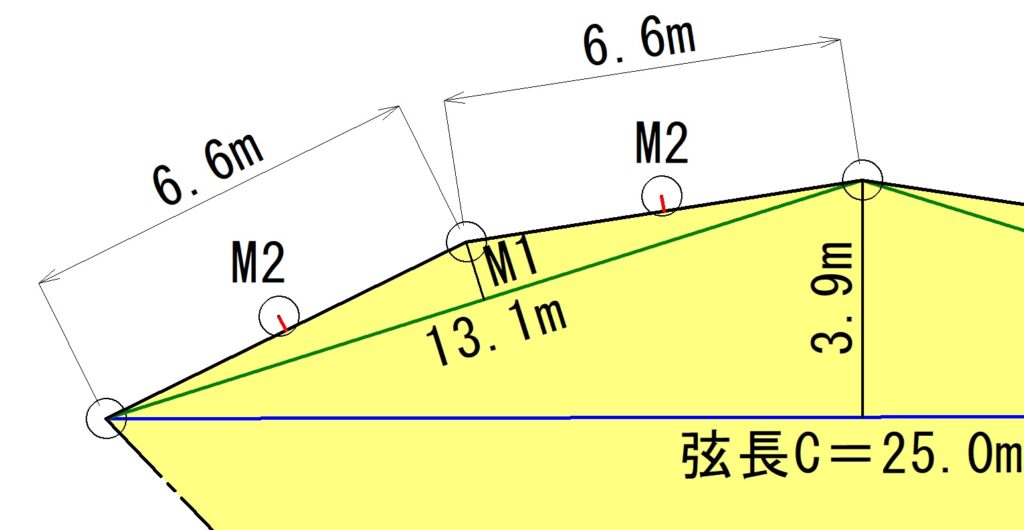
中央縦距【M2】は0.3ｍとなります。

Mをつなげて曲線を作ろう

これまで計算した中央縦距M、M1、M2の先端をつなげて曲線を作ります。

半径Rが大きい場合はM2÷4＝M3、M3÷４＝M4というように曲線上の点を多くすることで滑らかな曲線を作ることができます。

まとめ

土方カーブの計算方法について解説させていただきました。

弦長Cの中央縦距Mを計算して曲線の中間点を求めます。

土方カーブは手軽に現場で曲線を作ることができる方法です。

最後までお読みいただきありがとうございました。

あわせて読みたい

【土方カーブ】の計算方法｜三角関数で計算した数値と比較してみた

あわせて読みたい

単曲線【単カーブ】の記号・名称・公式について解説します

にほんブログ村

にほんブログ村

にほんブログ村

川下　政明

土木施工管理技士

XInstagramYouTube

川下政明（かわしもまさあき）と申します。
土木施工管理歴３０年。
地場の建設会社に勤務しております。
1級土木、2級管工事、2級舗装、測量士、採石業務管理者を保有しております。
このブログは、工事現場に関する「施工管理」・「測量」・「HO_CAD」・「JW-CAD」・「パソコン」などについて発信しています。
参考にしていただけると嬉しいです。