水の中でも書ける！現場の強い味方【測量野帳「耐水」LEVEL BOOK防水】｜セ-Y31B
まさあき
建設ナビ
PR
【後方交会法】２つの座標点から器械点座標の計算方法を解説
まさあき
記事内に商品プロモーションを含む場合があります
「後方交会法」の計算方法について解説します。
２つの既知点（座標点）から、任意の位置に据付けたトータルステーションの器械点XY座標「KP」を関数電卓で使って計算します。
この測量方法は、丁張設置などの現場測量におススメです。
あわせて読みたい
【座標「X,Y」】について解説します｜座標は位置を表す点（現場測量）
Contents
測量
トータルステーション（TS）を任意の場所に据付け、器械点「KP」とします。
既知点「T1」を視準し、水平角度を「０セット」します。そして水平距離「ｂ」を測定します。
次に既知点「T2」を視準して、水平角度「Ａ」と水平距離「ｃ」を測定します。
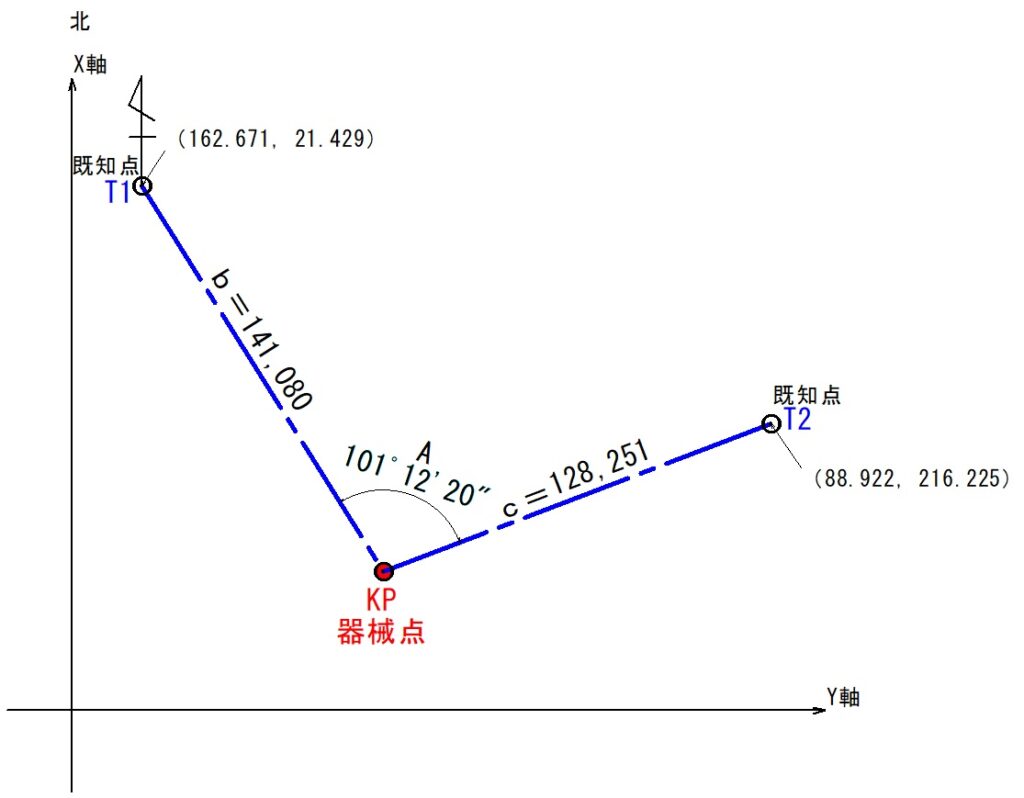
この測量結果から、器械点「KP」のXY座標を計算していきましょう。
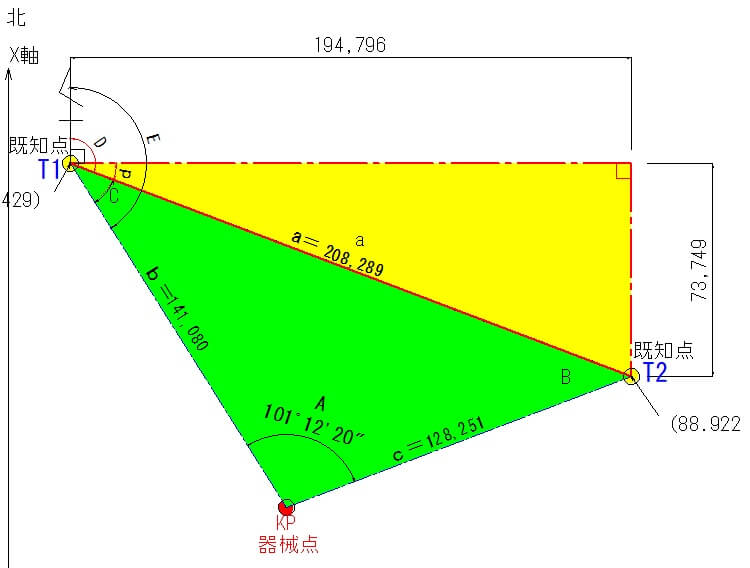
T1～T2間の距離「a」を算出
T1からT2までの水平距離「a」を、測量で実測した水平距離「ｂ」「ｃ」と水平角度「Ａ」から算出します。
算出方法は「余弦定理」です。
$$a^2=b^2+c^2-2bc cosA$$
この公式に測量した値を代入します。
$$a^2=141.080^2+128.251^2-2×141.080×128.251×cos101°12’20″$$
$$a^2=36351.885401-36187.30216×cos101.20555556$$
$$a=208.289$$
ということで、T1～T2までの距離「a」は208.289ｍとなりました。
角度「C」の計算
最初に角度「B」か「C」を正弦定理で算出します。
今回は「C」を計算してみましょう。
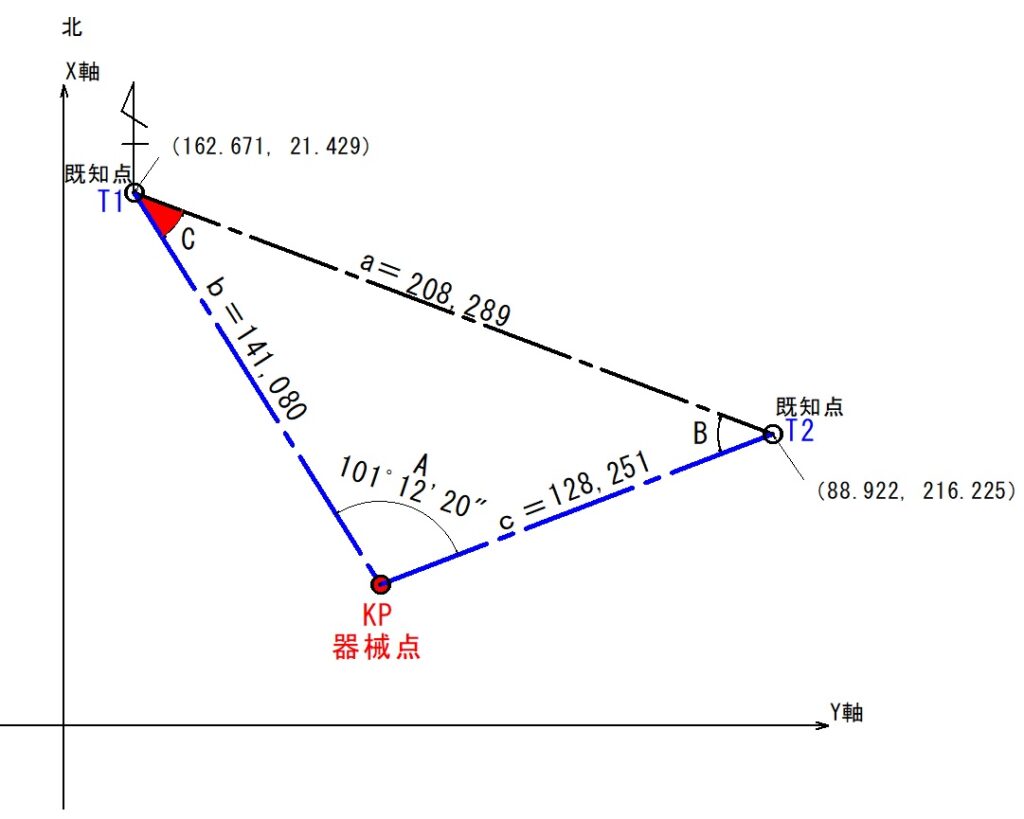
角度Cを正弦定理を使って算出します。
$$\frac{a}{sinA}=\frac{c}{sinC}$$
$$\frac{208.289}{sin101°12’20”}=\frac{128.251}{sinC}$$
$$\frac{128.251}{208.289}sin101.2055556=sinC$$
$$C=37.156746975=37°9’24″$$
ということで、角度「C」は37°9’24”となります。
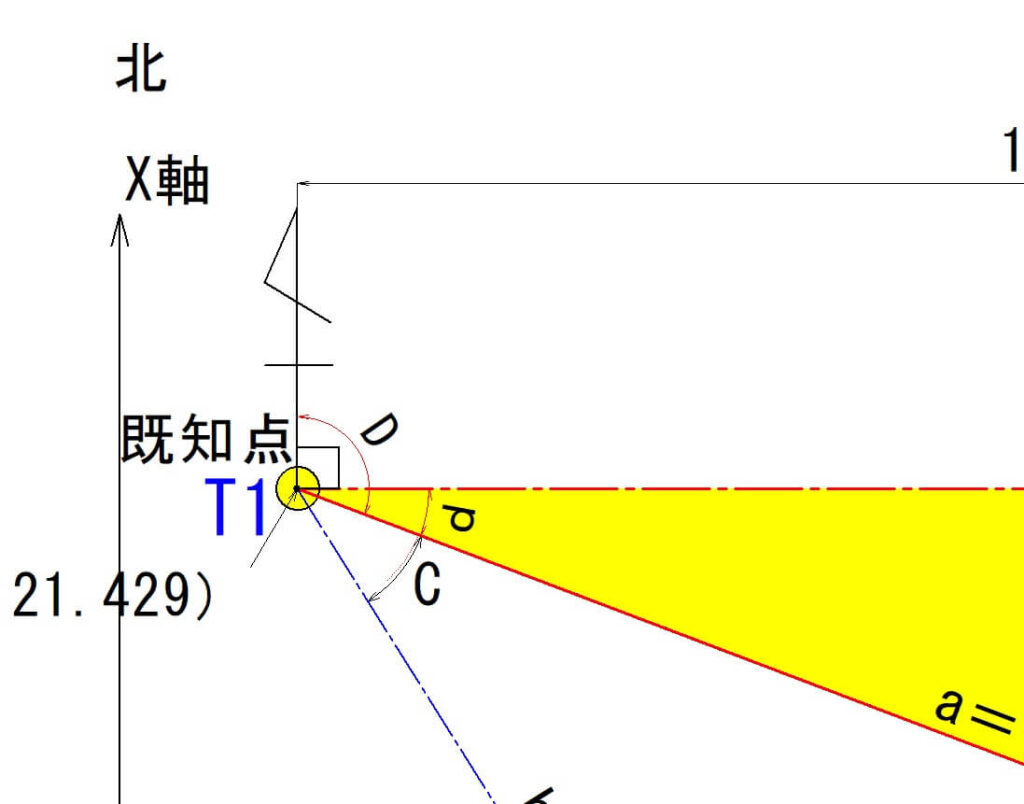
線「a」の方向角「D」の計算
方向角「D」を計算するには、方向角「D」＝ｄ＋90度からなるので、角度「ｄ」を三角関数で算出します。
T1の座標値： x=162.671,y=21.429
T2の座標値： x=88.922,y=216.225
直角三角形を作って、角度dを計算します。
T1とT2のx座標値の差とy座標値の差を計算して、直角三角形の縦と横の距離を計算します。
X=162.671-88.922=73.749m
Y=216.225-21.429=194.796m
$$tand=\frac{73.749}{194.796}$$
$$d=20°44’11″$$
方向角D＝ｄ+90
$$D=20°44’11″+90=110°44’11″$$
ということで、【方向角D＝110°44′11″】となります。
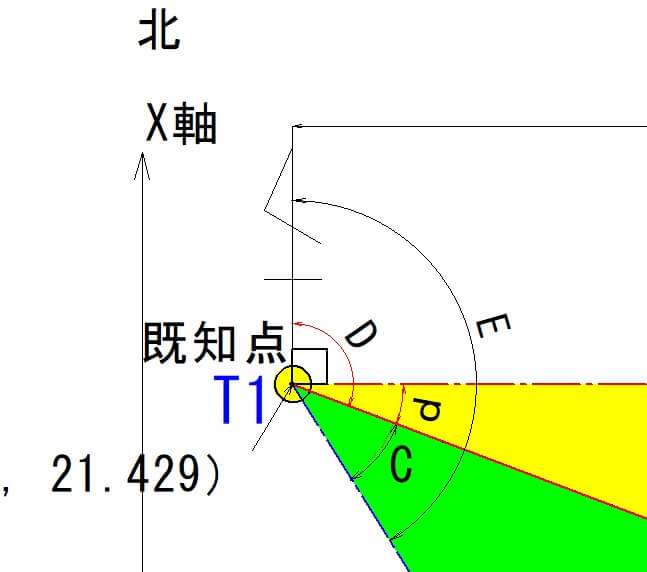
線「ｂ」の方向角「E」の計算
角度「C」と方向角「D」を合わせて、線「ｂ」の方向角「Ｅ」を計算します。
$$E=C+D=37°9’24″+110°44’11″=147°53’35″$$
したがって、線「b｣の方向角「E」は147°53′35″となります。
T1からKPまでのXY軸距離「KPx」と「KPy」の計算
方向角「E」から器械点「KP」の座標を計算します。
角度「F」を求めて、三角関数でT1からKPまでのXY軸距離「KPx」と「KPy」を算出しましょう。
角度Fの計算
最初に角度「Ｆ」から求めます。
$$F=180°-E=180°-147°53’35″$$
$$F=32°6’25″$$
T1からKPまでのY軸距離の計算
次にKPyを求めます。
$$sinF=\frac{KPy}{b}$$
$$sin32°6’25″=\frac{KPy}{141.080}$$
$$KPy=74.984$$
ということで「KPy」＝74.984ｍとなります。
T1からKPまでのX軸距離の計算
続いてKPxを求めます。
$$cosF=\frac{KPx}{b}$$
$$cos32°6’25″=\frac{KPx}{141.080}$$
$$KPx=119.503$$
ということで、「KPx」＝119.503ｍとなります。
器械点「KP」の座標計算
最後に基準となった「Ｔ１」のＸＹ座標から「KPx」と「KPy」をそれぞれ加えて「KP」の座標を算出しましょう。
T1から見て「KPx」は下向きなので「マイナス」します。
T1から見て「KPy」は右向きなので「プラス」します。
$$ＫＰのＸ座標=162.671-119.503＝43.168$$
$$ＫＰのＹ座標＝21.429+74.984＝96.413$$
器械点座標「KP」の計算結果
ということで、器械点「ＫＰ」の座標は
X＝43.168
Y＝96.413
となります。
あわせて読みたい
座標点【3点】から器械点座標値を計算してみよう｜【後方交会法】
おわりに
このブログでは後方交会法の計算方法についてお話ししました。
「後方交会法」は２点の既知点（座標点）から任意に据付けした「器械点の座標」を求める測量です。
この測量は後視２点までの角度と距離を使って計算するので、計算上の誤差を含む可能性があります。
土工事などの現場測量に利用して、正確さを要する構造物などの測量は、座標点に器械を設置して測量することをおススメします。
今回使用した公式は「正弦定理」「余弦定理」「三平方の定理」「三角関数」の４つになります。
皆様の参考になれば幸いです。
最後まで読んでいただきありがとうございました。
 にほんブログ村 |
 にほんブログ村 |
 にほんブログ村 |
ABOUT ME
川下政明（かわしもまさあき）と申します。
土木施工管理歴３０年。
地場の建設会社に勤務しております。
1級土木、2級管工事、2級舗装、測量士、採石業務管理者を保有しております。
このブログは、工事現場に関する「施工管理」・「測量」・「HO_CAD」・「JW-CAD」・「パソコン」などについて発信しています。
参考にしていただけると嬉しいです。
土木施工管理歴３０年。
地場の建設会社に勤務しております。
1級土木、2級管工事、2級舗装、測量士、採石業務管理者を保有しております。
このブログは、工事現場に関する「施工管理」・「測量」・「HO_CAD」・「JW-CAD」・「パソコン」などについて発信しています。
参考にしていただけると嬉しいです。
