【後方交会法】２つの座標点から器械点座標の計算方法を解説
まさあき
建設ナビ
PR
【バーチカル曲線】縦断曲線の計算方法をわかりやすく解説します
まさあき
記事内に商品プロモーションを含む場合があります
道路設計や施工に関与する者にとって、「バーチカル曲線」は非常に重要な概念です。
これは、道路の縦断勾配の変化点で利用され、乗用車やバイクが道路を滑らかに通過できるようにするためのものです。
しかし、この曲線を正確に計算・設定するには、一定の公式や手法が必要です。
この記事では、バーチカル曲線とは何か、その計算方法や公式、そして実際の計算例を通じて、その重要性と適切な設定方法を詳しく解説します。
道路設計や施工の専門家だけでなく、関心を持つ読者にとっても役立つ情報が満載です。
さぁ、一緒にバーチカル曲線の奥深い世界を探求してみましょう。
バーチカル曲線とは
道路の縦断勾配の変化点に曲線を挿入し、徐々に勾配を変化させて車やバイクがスムーズに走れるようにする曲線です。
この曲線を「縦断曲線」または「バーチカルカーブ(vertical curve)」とも言います。
公式
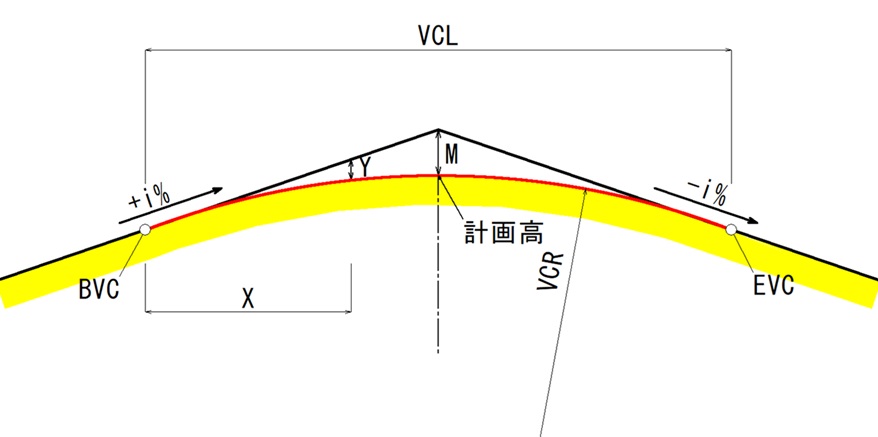
標準的な縦断図です。
左側から「i1%」の上り坂を登ってきて、右側「i2%」の下り坂を降りていくイメージ図です。
$$M=\frac{(i1-i2)}{800}×VCL$$
$$Y=\frac{(i1-i2)}{(200×VCL)}X^2$$
$$VCR=\frac{VCL}{i}$$
$$VCL=VCR×i$$
VCL:縦断曲線長（縦断曲線を設置する区間）
VCR:縦断曲線半径
i : 勾配(前後の勾配の差）
実際に計算してみよう
例として計画縦断図を作成しました。
２つのバーチカル曲線が入っていますので一つ一つ計算してみましょう。
№2のバーチカル（VCL＝20.000）の計算
詳細縦断図です。
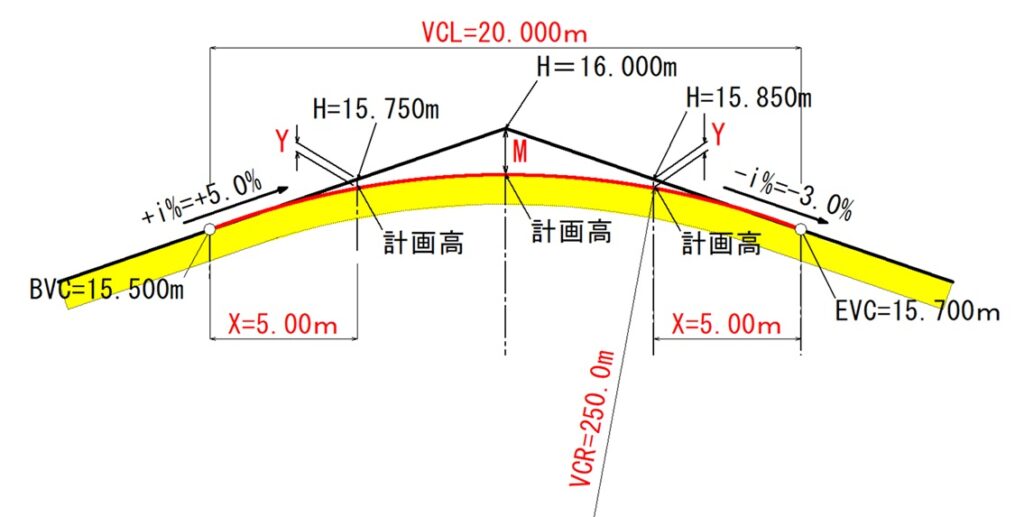
丁張を5ｍピッチで設置するものとして、5.0％での№1+15.0の値を計算します。
$$5.00ｍ×0.05＝0.250ｍ$$
$$15.500（BVC）+0.250＝15.750ｍ$$
となります。
続いて、№2の16.000から-3.0％での№2+5.0の値を計算します。
$$5.00ｍ×（-0.03）＝-0.150ｍ$$
$$16.000+（-0.150）＝15.850ｍ$$
となります。
「M」と「Y」の値を先ほど紹介した公式より算出します。
$$M=\frac{(i1-i2)}{800}×VCL=\frac{(5.0-(-3.0))}{800}×20.000=0.200m$$
ということで、M＝0.200ｍとなります。
$$Y=\frac{(i1-i2)}{(200×VCL)}X^2=\frac{(5.0-(-3.0))}{(200×20.000)}×5.000^2=0.050m$$
ということで、Y＝0.050ｍとなります。
では、№2の16.000からMを引き算して計画高さを求めます。
$$№2の計画高＝16.000-0.200=15.800m$$
したがって、№2の計画高さは15.800ｍとなります。
次に№1+15.0・№2+5.0の計画高を計算します。
№1+15.0の「15.750ｍ」からＹを引き算します。
$$№1+15.0の計画高＝15.750-0.050=15.700ｍ$$
№2+5.0の「15.850ｍ」からＹを引き算します。
$$№2+5.0の計画高＝15.850-0.050=15.800ｍ$$
となります。
ちなみに、バーチカル曲線の頂点は№2+2.5ｍ付近になります。
VCR（縦断曲線半径）を求めます。
ここでの計算は、勾配を5.0％＝0.050、3.0％＝0.030として行います。
$$VCR=\frac{VCL}{i}＝\frac{20.000}{(0.050-(-0.030))}＝250.0ｍ$$
となります。
№3+10.0のバーチカル（VCL＝10.000）の計算
詳細縦断図です。
丁張を2.5ｍピッチで設置するものとして、-3.0％での№3+7.5の値を計算します。
$$2.50ｍ×（-0.03）＝-0.075ｍ$$
$$15.250（BVC）+（-0.075）＝15.175ｍ$$
となります。
続いて、№3+10.0の15.100mから-1.0％での№3+12.5の値を計算します。
$$2.50ｍ×（-0.01）＝-0.025ｍ$$
$$15.100+（-0.025）＝15.075ｍ$$
となります。
「M」と「Y」の値を公式より算出します。
$$M=\frac{(i1-i2)}{800}×VCL=\frac{(（-3.0）-(-1.0))}{800}×10.000=-0.025m$$
ということで、M＝-0.025ｍとなります。
$$Y=\frac{(i1-i2)}{(200×VCL)}X^2=\frac{((-3.0)-(-1.0))}{(200×10.000)}×2.500^2=-0.006m$$
ということで、Y＝-0.006ｍとなります。
では、№3+10.0の15.100からMを引き算して計画高さを求めます。
$$№3+10.0の計画高＝15.100-(-0.025)=15.125$$
したがって、№3+10.0の計画高さは15.125ｍとなります。
次に№3+7.5・№3+12.5の計画高を計算します。
№3+7.5の「15.175ｍ」からＹを引き算します。
$$№3+7.5の計画高＝15.175-(-0.006)=15.181ｍ$$
№3+12.5の「15.075ｍ」からＹを引き算します。
$$№3+12.5の計画高＝15.075-(-0.006)=15.081ｍ$$
となります。
VCR（縦断曲線半径）を求めます。
ここでの計算は、勾配を3.0％＝0.030、1.0％＝0.010として行います。
$$VCR=\frac{VCL}{i}＝\frac{10.000}{((-0.030)-(-0.010))}＝500.0ｍ$$
となります。
終わりに
このブログでは、「バーチカル曲線」の計算方法について解説しました。
公式は次の通りです。
$$M=\frac{(i1-i2)}{800}×VCL$$
$$Y=\frac{(i1-i2)}{(200×VCL)}X^2$$
$$VCR=\frac{VCL}{i}$$
$$VCL=VCR×i$$
VCL:縦断曲線長（縦断曲線を設置する区間）
VCR:縦断曲線半径
i : 勾配(前後の勾配の差）
現場で使える計算式ですので、丁張設置の際に使っていただければ幸いです。
丁張設置後は、必ず自分の目で丁張全体を見通してみましょう。
計算が間違っている場合はすぐにわかるチェック方法です。
最後まで読んでいただきありがとうございました。
 にほんブログ村 |
 にほんブログ村 |
 にほんブログ村 |
ABOUT ME
川下政明（かわしもまさあき）と申します。
土木施工管理歴３０年。
地場の建設会社に勤務しております。
1級土木、2級管工事、2級舗装、測量士、採石業務管理者を保有しております。
このブログは、工事現場に関する「施工管理」・「測量」・「HO_CAD」・「JW-CAD」・「パソコン」などについて発信しています。
参考にしていただけると嬉しいです。
土木施工管理歴３０年。
地場の建設会社に勤務しております。
1級土木、2級管工事、2級舗装、測量士、採石業務管理者を保有しております。
このブログは、工事現場に関する「施工管理」・「測量」・「HO_CAD」・「JW-CAD」・「パソコン」などについて発信しています。
参考にしていただけると嬉しいです。
