【スタッフ】の読み方をわかりやすく解説します
まさあき
建設ナビゲーター
PR
座標点【3点】から器械点座標値を計算してみよう｜【後方交会法】
まさあき
記事内に商品プロモーションを含む場合があります
「後方交会法」の計算方法について解説します。
３つの既知点（座標点）から、任意に据付けたトータルステーション（TS）の位置（座標）を関数電卓を使って計算します。
この測量方法の大きな利点として、「２つの既知点からの後方交会法」よりも精度が高いことです。
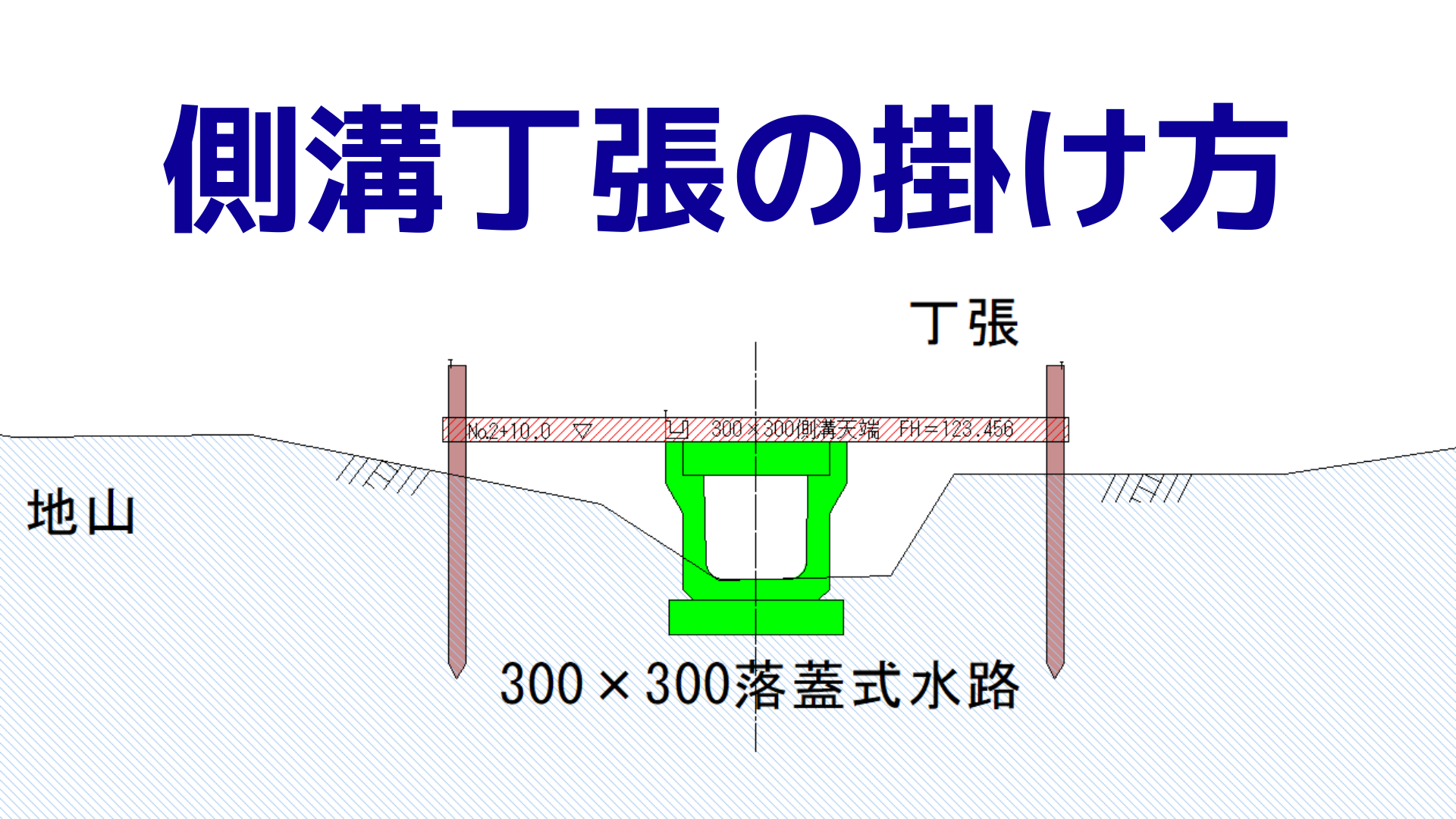
そして、トータルステーションを測量しやすい場所に据え付けすることができるので、障害物の多い現場や土工事の丁張設置などの現場測量におススメです。
「２つの既知点からの後方交会法」についてはこちらのブログを参考にしてください。
あわせて読みたい
【後方交会法】入門：２つの座標点から器械点座標の計算方法ガイド
Contents
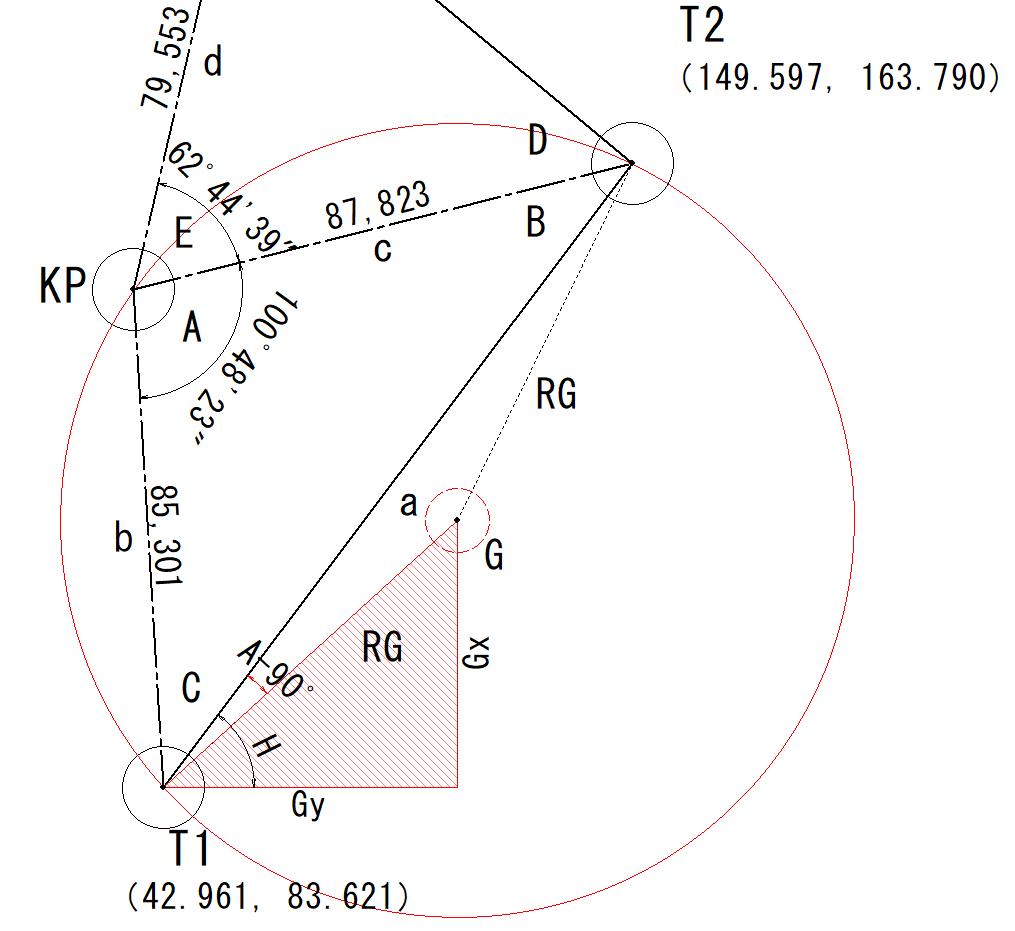
測量データ
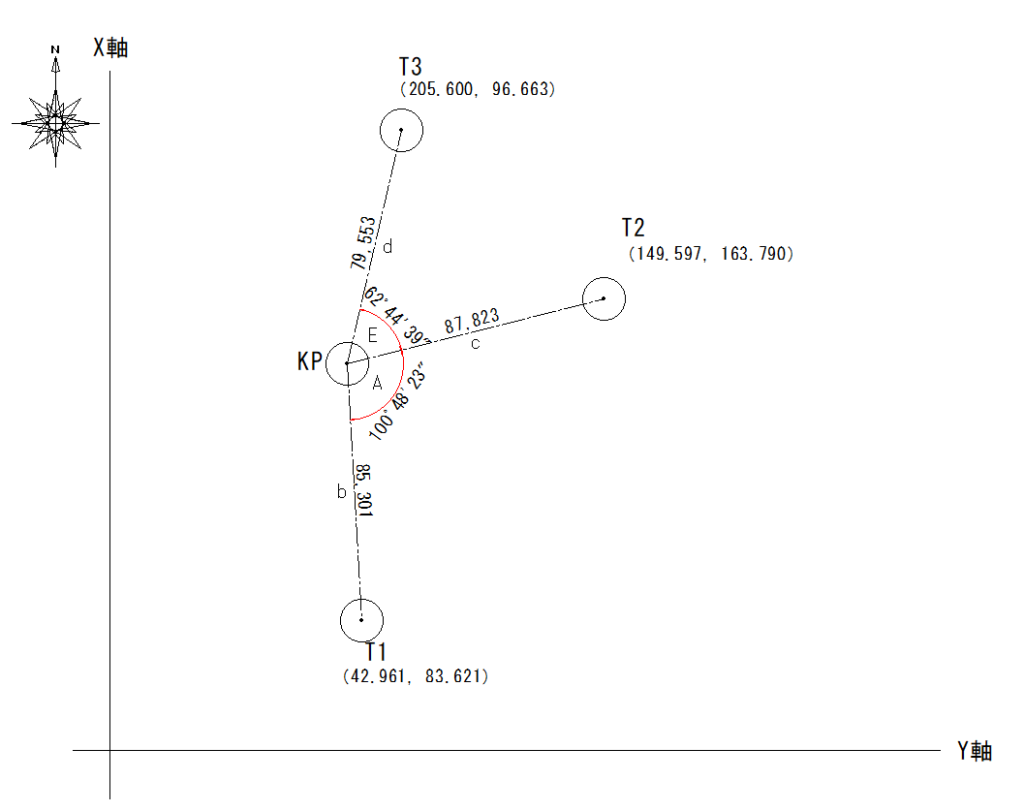
最初にトータルステーション（TS）を任意の場所に据付けます。
そのトータルステーションを据え付けたポイントを、器械点「KP」とします。
既知点「T3」を視準し、水平角度を「０セット」します。
そして水平距離「d」を測定します。
次に既知点「T2」を視準して、水平角度「E」と水平距離「ｃ」を測定します。
最後に、既知点「T1」を視準して、水平角度「A」と水平距離「ｂ」を測定します。
このように、既知点「T3」→「T2」→「T1」の順で、3点を測量します。
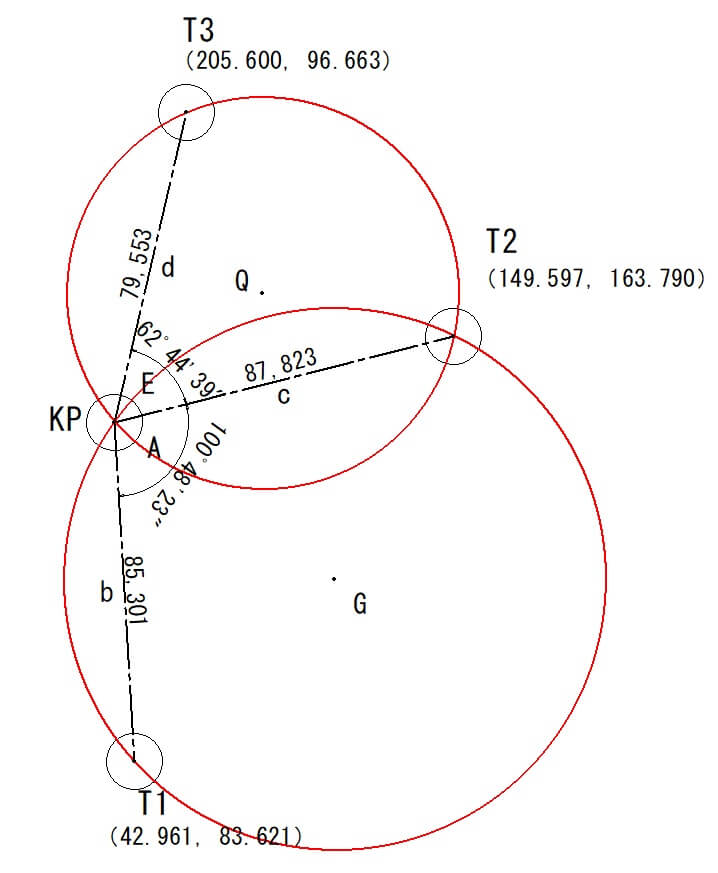
下の図は、T1～T3の座標値と測量した水平角度と水平距離を表示したものです。
| 基準点名 | X座標 | Y座標 | 水平角度 | 距離 |
| T3 | 205.600m | 96.663m | 0 | 79.553m |
| T2 | 149.597m | 163.790m | 62°44′39″ | 87.823m |
| T1 | 42.961m | 83.621m | 163°33′2″ | 85.301m |
水平角度A＝163°33′2″-62°44′39″＝100°48′23″
あわせて読みたい
【座標「X,Y」】について解説します｜座標は位置を表す点（現場測量）
2つの外接円を作成
下の図のように、KPとT3,T2を通る外接円とKPとT2,T1を通る外接円、この２つの円を作成します。
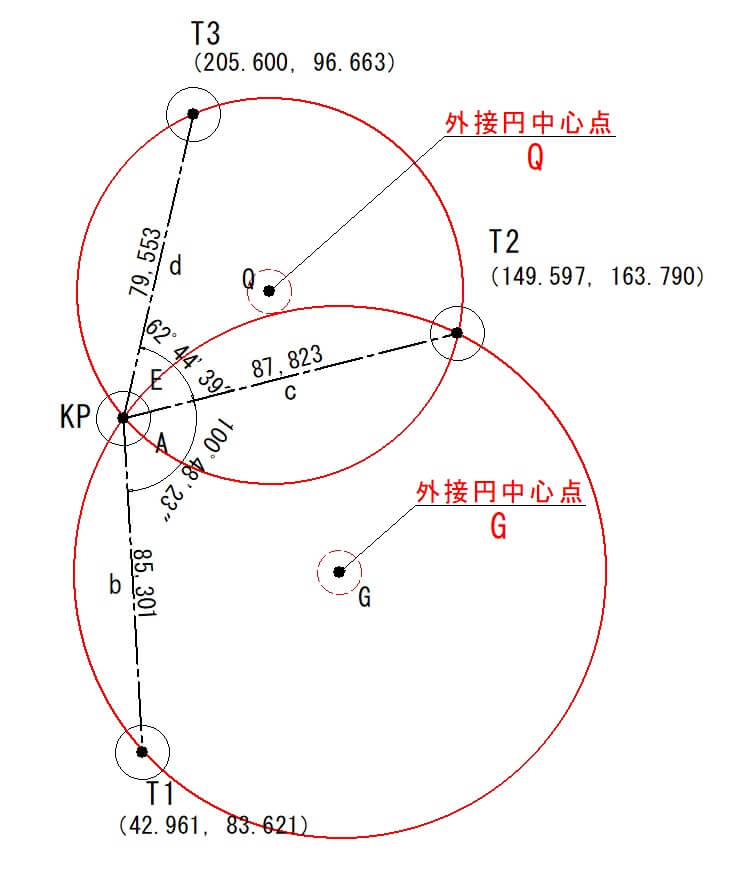
外接円中心点の座標計算
外接円の中心点（G、Q）の座標値を計算しましょう。
外接円中心「G」の座標計算
T1～T2間の「a」の計算
最初にT1とT2の座標間の距離「a」を計算します。
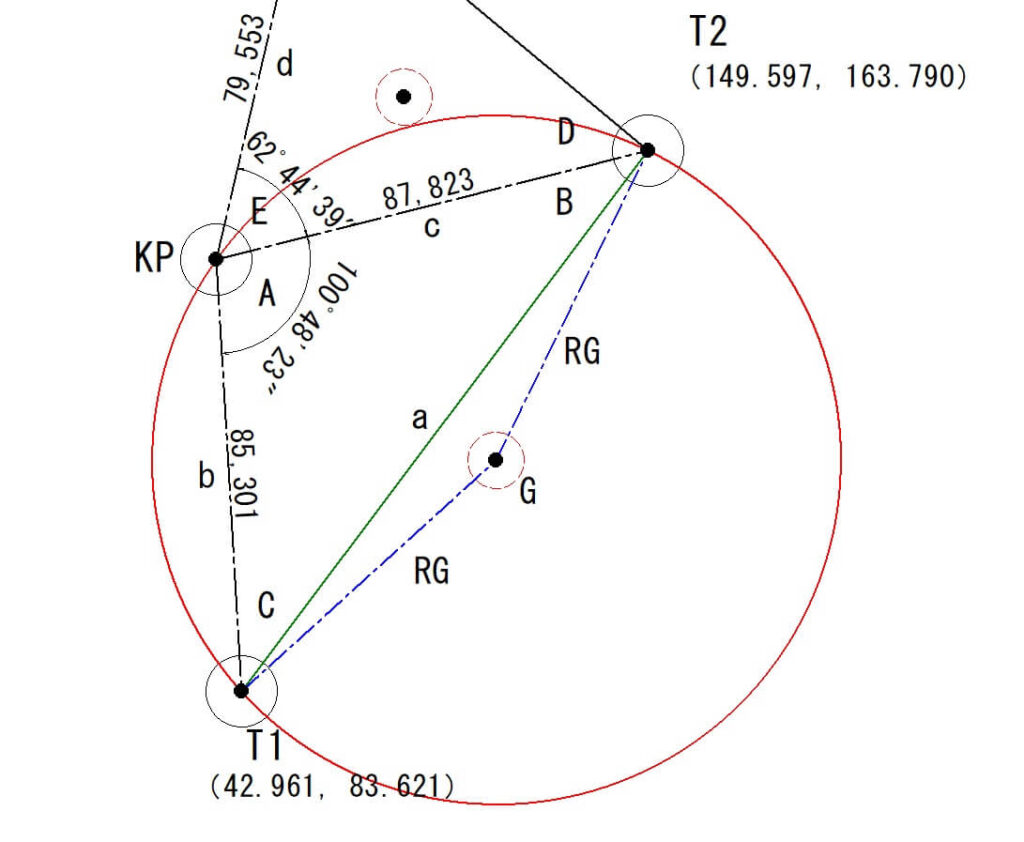
aを計算するには、T1とT2のX座標値とY座標の差を計算して三平方の定理で求めます。
X座標の差＝149.597-42.961=106.636
Y座標の差＝163.790-83.621=80.169
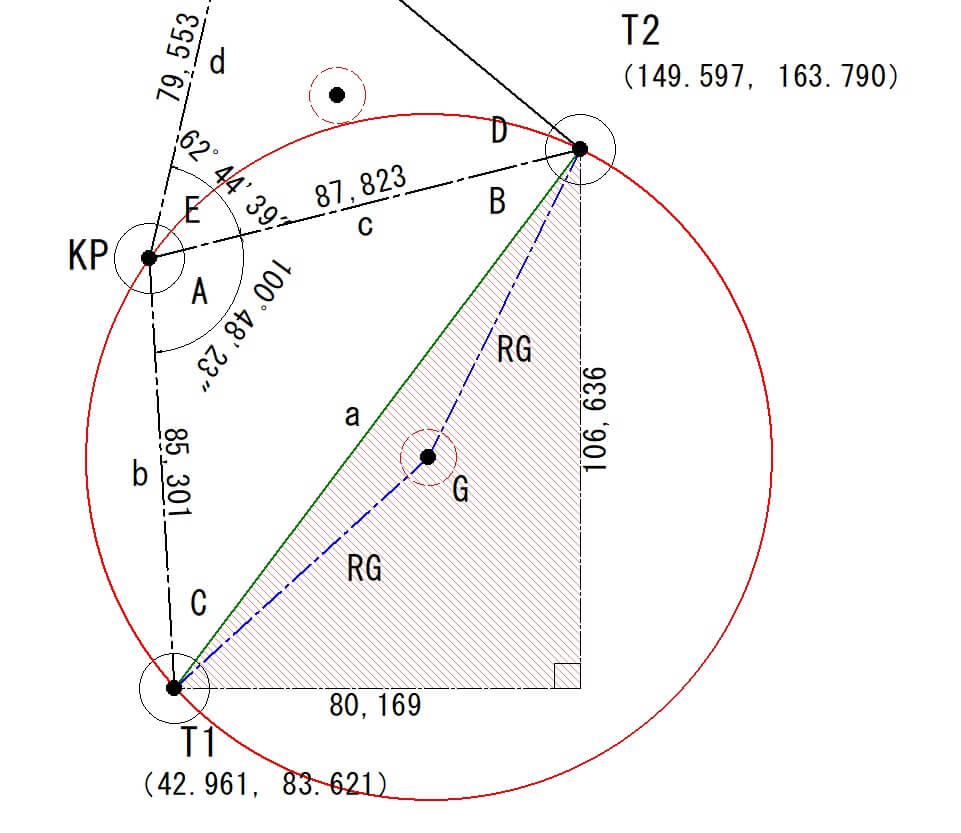
「Ｘ」と「Ｙ」の差から三平方の定理で「a」を算出します。
$$a=\sqrt{(106.636^2)+(80.169^2)}$$
$$a=133.410$$
T1とT2間の距離「a」は133.410mとなります。
半径RGの計算
先ほど計算した「a」を使って、半径「RG」を正弦定理で求めます。
正弦定理の公式は次の通りです。
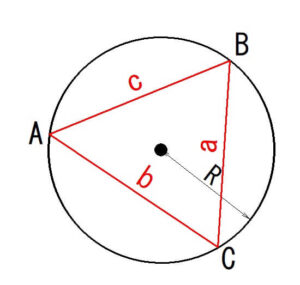
$$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$$
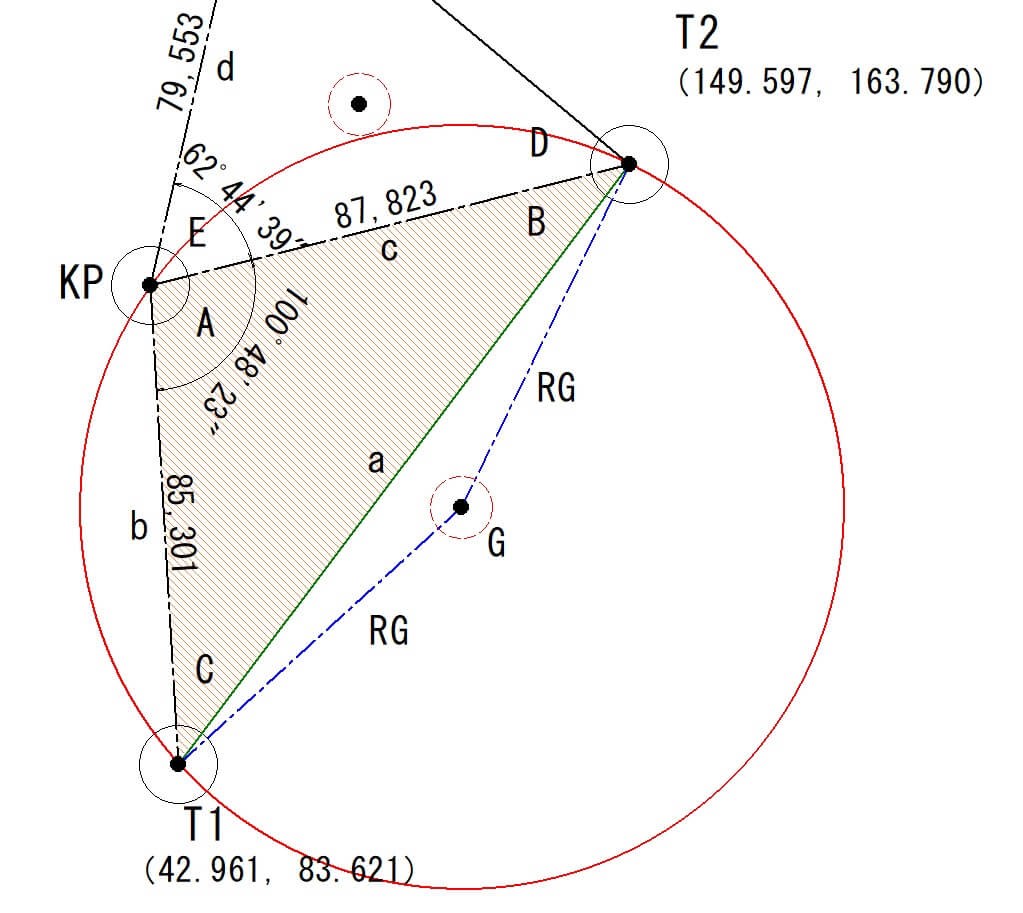
半径RGを計算してみましょう。
$$\frac{a}{sinA}=2RG$$
$$RG=\frac{133.410}{2×sin100°48’23”}$$
$$RG=67.909$$
したがって半径RG＝67.909ｍとなります。
角度Hの計算
次にT1のY軸と線aの角度「H」を計算します。
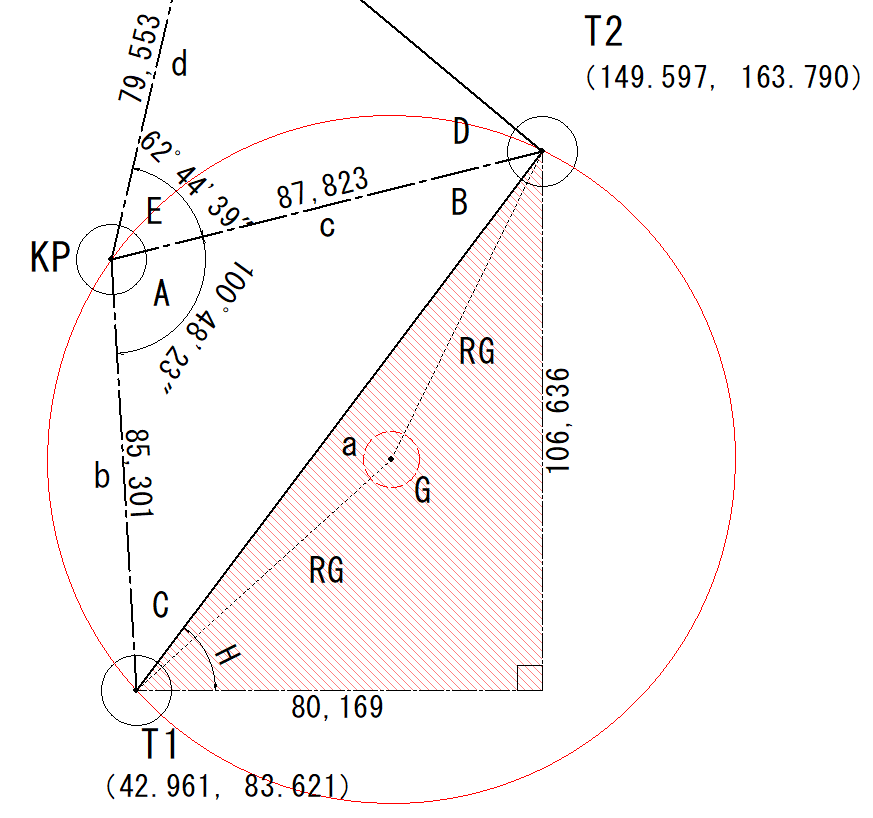
三角関数を使います。
$$tanH=\frac{106.636}{80.169}$$
$$H=53°3’51″$$
となります。
T1から中心点GまでのX軸の計算
T1から中心点GまでのXY座標値計算
次に外接円中心点Gの座標を計算します。
中心点Gを計算するには「円に接する四角形の性質」を使用します。
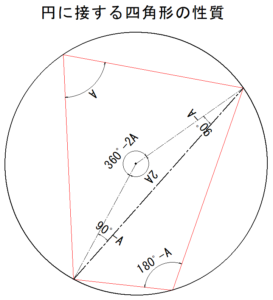
半径RG＝67.909ｍ
H=53°3’51”
A=100°48′23″
$$Gx=RGsin(H-(A-90°))$$
$$Gx=67.909sin(53°3’51”-(100°48’23”-90))$$
$$Gx=45.667$$
T1から中心点GまでのY軸の計算
$$Gy=RGcos(H-(A-90°))$$
$$Gy=67.909cos(53°3’51”-(100°48’23”-90))$$
$$Gy=50.261$$
中心点G座標値
基準となったT1の座標値(42.961,83.621)にGxとGyを加えていきます。
GⅹはT1より上側なので「プラス」。
GyはT1より右側なので「プラス」となります。
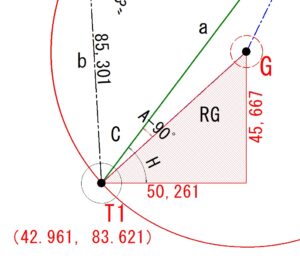
$$GX=42.961+45.667=88.628$$
$$GY=83.621+50.261=133.882$$
したがって、中心点Gの座標値は(X＝88.628,Y＝133.882)となります。
外接円中心「Q」の座標計算
T2～T3間の「e」の計算
T2とT3の座標間の距離「e」を計算します。
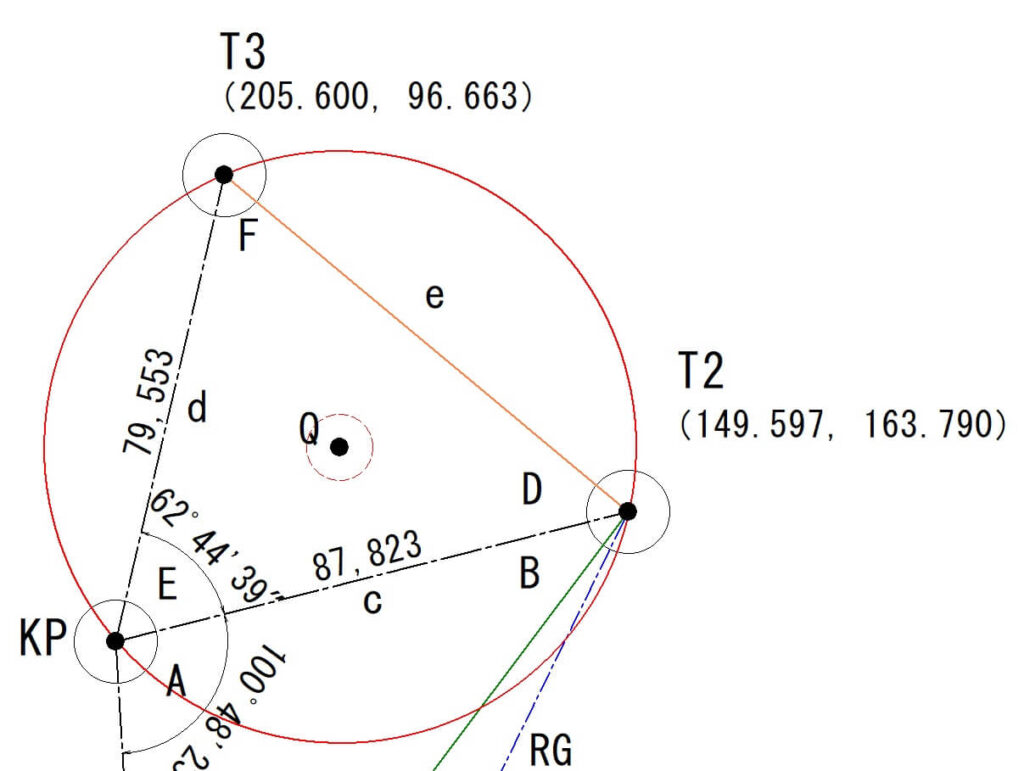
eを計算するには、T2とT3のX座標値とY座標の差を計算して三平方の定理で求めます。
X座標の差＝205.600-149.597=56.003
Y座標の差＝163.790-96.663=67.127
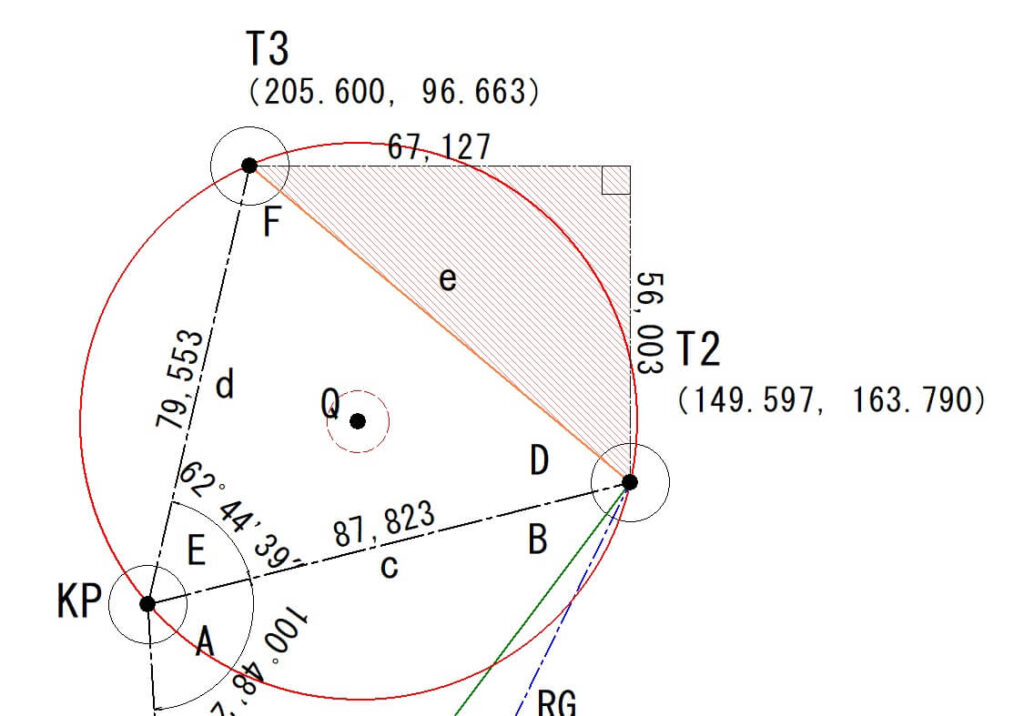
「Ｘ」と「Ｙ」の差から三平方の定理で「e」を算出します。
$$e=\sqrt{(56.003^2)+(67.127^2)}$$
$$e=87.421$$
T2とT3間の距離「e」は87.421mとなります。
半径RQの計算
次に、中心「Q」の外接円の半径を正弦定理で求めます。
$$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$$
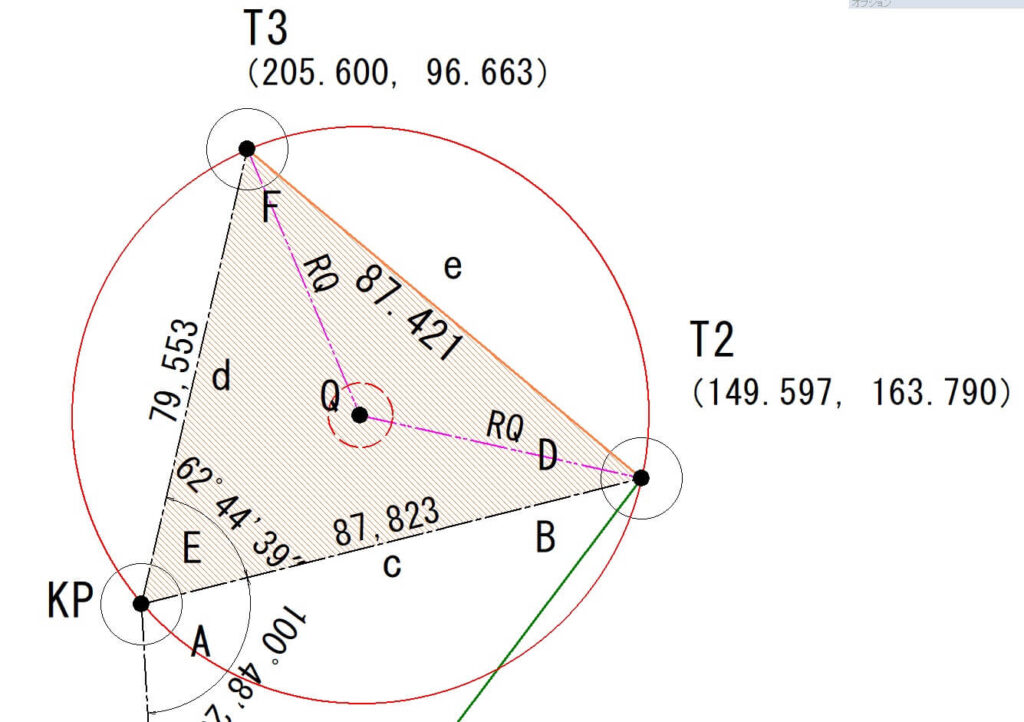
半径RQを計算してみましょう。
$$\frac{e}{sinE}=2RQ$$
$$RQ=\frac{87.421}{2×sin62°44’39”}$$
$$RQ=49.170$$
したがって、半径RQ＝49.170ｍとなります。
角度Iの計算
次にT3のY軸と線eの角度「I」を計算します。
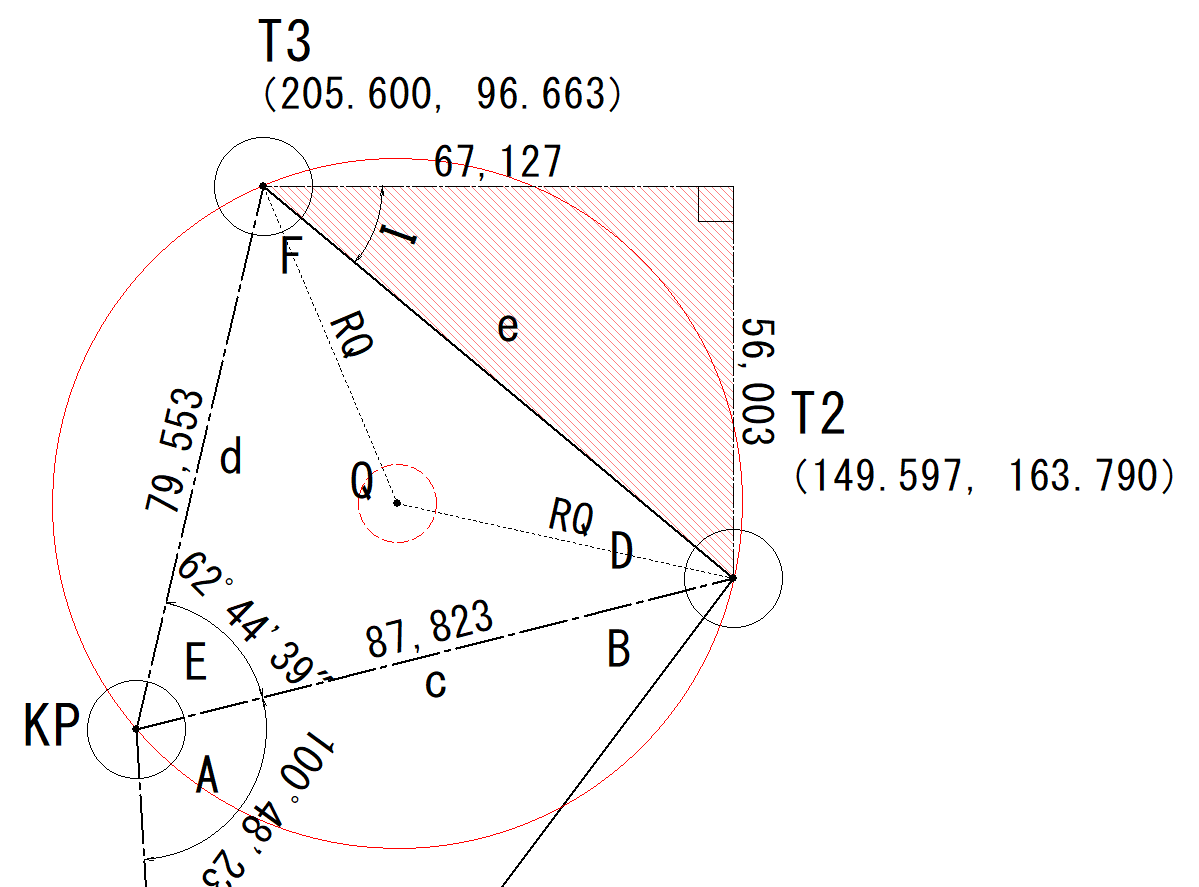
三角関数を使います。
$$tanI=\frac{56.003}{67.127}$$
$$I=39°50’16″$$
T3から中心点Qまでの距離Xの計算
次に外接円中心点Qまでの距離(XY座標)を計算します。
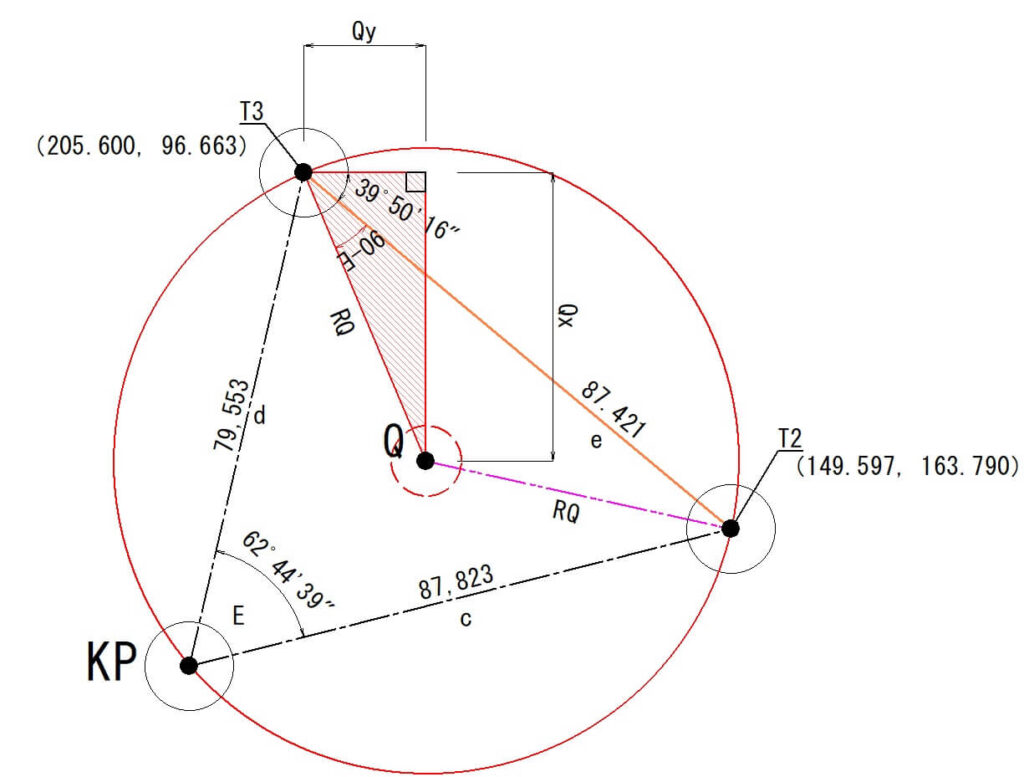
$$Qx=RQsin(I+(90°-E))$$
$$Qx=49.170sin(39°50’16″+(90°-62°44’39”))$$
$$Qx=45.293$$
T3から中心点Qまでの距離Yの計算
$$Qy=RQcos(I+(90°-E))$$
$$Qy=49.170cos(39°50’16″+(90°-62°44’39”))$$
$$Qy=19.138$$
中心点Q座標値
基準となったT3の座標値にそれぞれ加えていきます。
QⅹはT3より下側なので「マイナス」。
QyはT3より右側なので「プラス」となります。
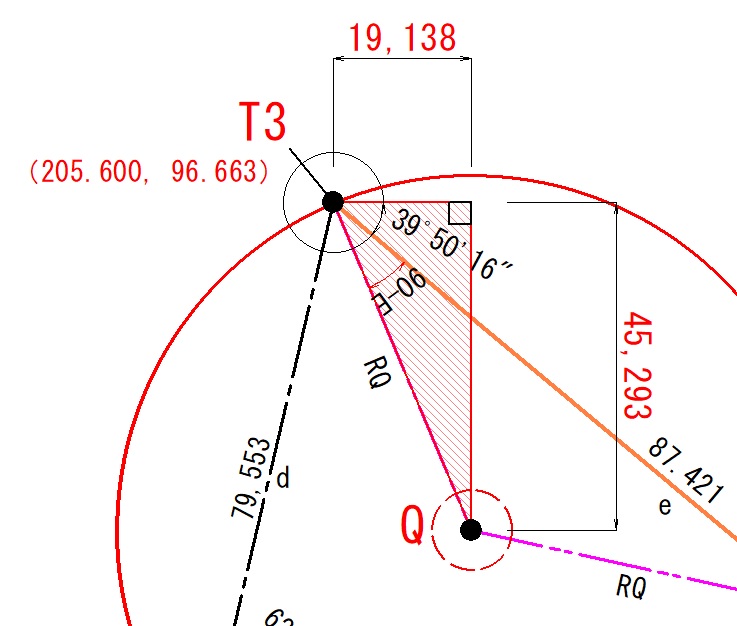
$$QX=205.600-45.293=160.307$$
$$QY=96.663+19.138=115.801$$
したがって、中心点Qの座標値は(X＝160.307,Y＝115.801)となります。
２つの外接円中心座標から器械点（KP）を求める
- 2つの円中心点間距離「ｓ」の計算
- 次に角度「Ｊ」の計算、
- 角度「Ｋ」の計算、
- 最後に器械点「ＫＰ」の座標値計算という流れになります。
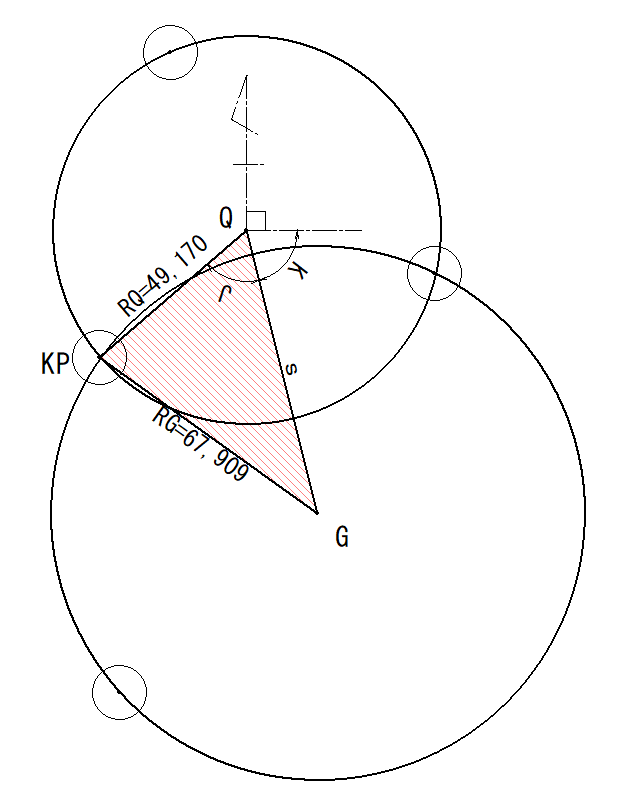
外接円中心点間距離「ｓ」の計算
G(88.628,133.882)とQ(160.307,115.801)のそれぞれ「Ｘ」と「Ｙ」の差を計算します。
$$GX-QX=88.628-160.307=-71.679$$
$$GY-QY=133.882-115.801=18.081$$
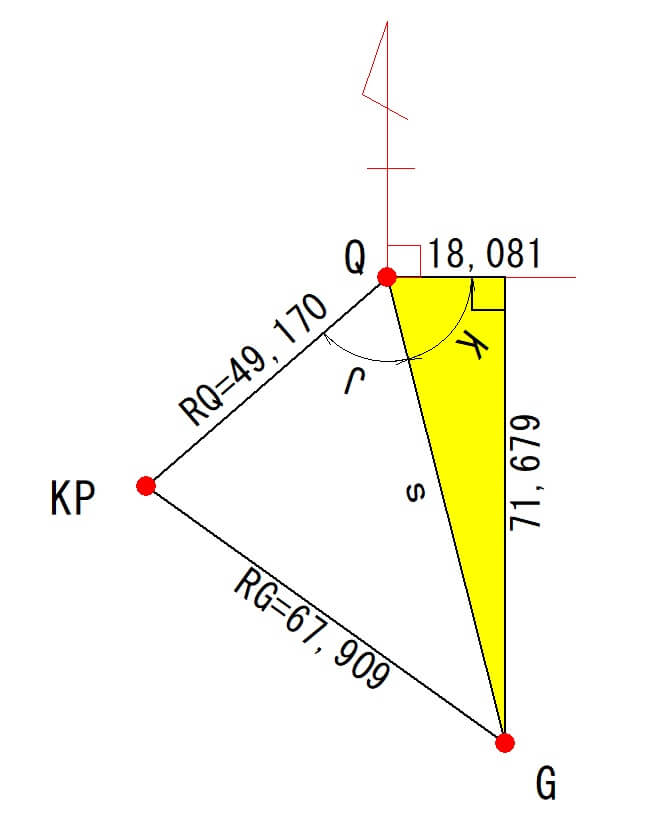
「Ｘ」と「Ｙ」の差から三平方の定理で「s」を算出します。
$$s=\sqrt{(-71.679^2)+(18.081^2)}$$
$$s=73.924$$
したがって、距離「s」は73.924ｍとなります。
角度「Ｊ」の計算
算出方法は「余弦定理」です。
公式は次の通りです。
$$a^2=b^2+c^2-2bc cosA$$
$$b^2=a^2+c^2-2ac cosB$$
$$c^2=a^2+b^2-2ab cosC$$
この公式に値を代入します。
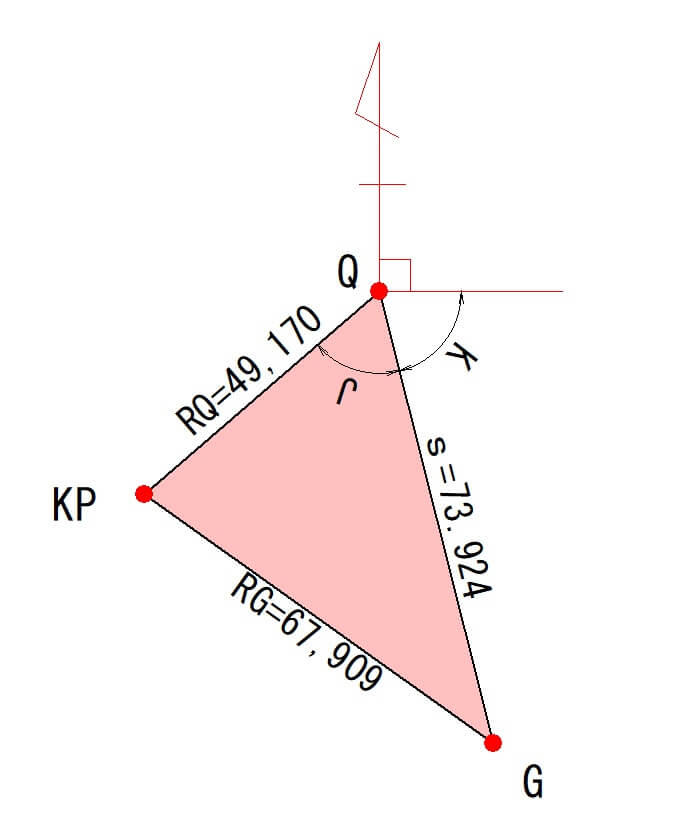
$$RG^2=s^2+RQ^2-2sRQ cosJ$$
$$67.909^2=73.934^2+49.170^2-2×73.924×49.170×cosJ$$
$$J=63°15’40″$$
したがって、角度「Ｊ」は63°15’40″となります。
角度「Ｋ」の計算
中心点座標Q(160.307,115.801)と、中心点座標G(88.628,133.882)のXY座標値の差を求めて、三角関数で計算します。
X＝160.307-88.623＝71.679
Y＝133.882-115.801＝18.081
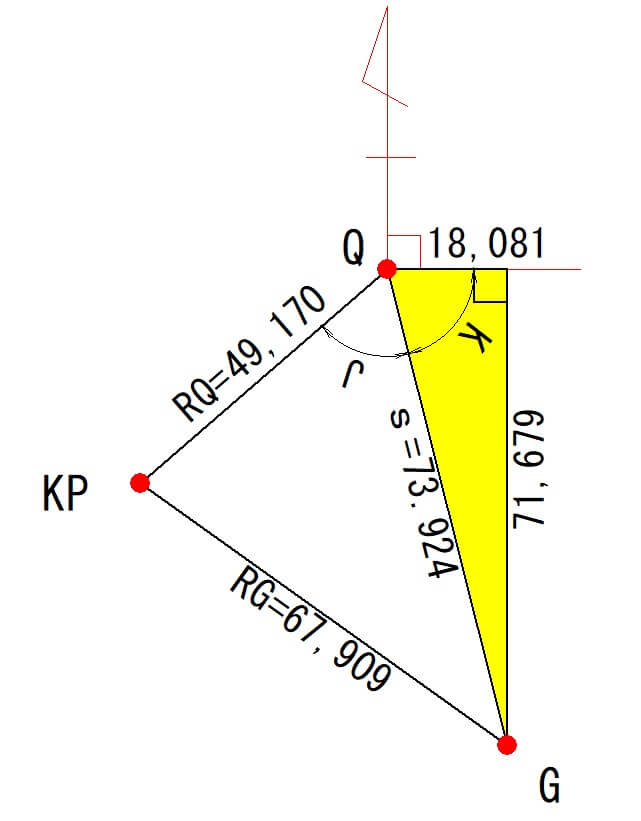
$$tanK=\frac{71.679}{18.081}$$
$$K=75°50’33″$$
したがって、角度「K」は75°50’33″となります。
器械点「KP」の座標計算
角度ｍの計算
先ほど計算した「K」と「J」を使って、角度「m」を計算します。
m=180°-J-K
＝180°-63°15′40″-75°50′33″
＝40°53′47″
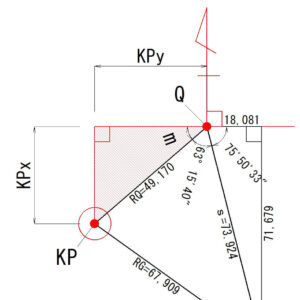
中心点QからKPまでの距離Xの計算
角度「m」を使い三角関数でKPxを計算します。
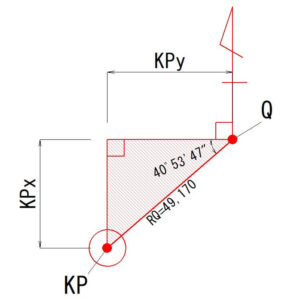
$$\frac{KPx}{49.170}=sin(40°53′47″)$$
$$KPx=32.191$$
中心点QからKPまでの距離Yの計算
角度「m」を使い三角関数でKPyを計算します。
$$\frac{KPy}{49.170}=cos(40°53′47″)$$
$$KPy=37.167$$
器械点KPの座標値
基準となった中心点「Q」の座標値にKPxとKPyそれぞれ加えていきます。
KPxは中心点Qより下側なので「マイナス」。
KPyは中心点Qより左側なので「マイナス」します。
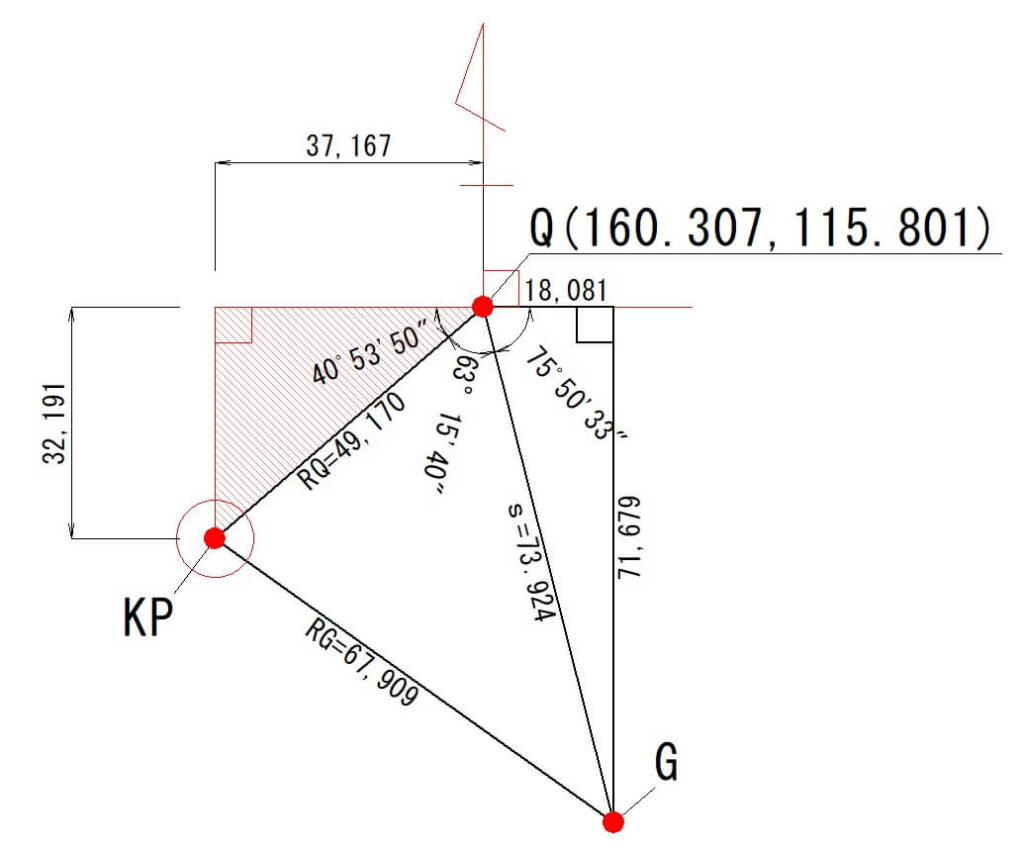
$$KPX=160.307-32.191=128.116$$
$$KPY=115.801-37.167=78.634$$
したがって、器械点「KP」の座標値は(X＝128.116,Y＝78.634)となります。
おわりに
最後まで読んでいただきありがとうございました。
３点の既知点（座標点）から任意の器械点を求める後方交会法の計算方法を解説いたしました。
この計算方法は既知点を通る2つの円を作り、円の中心点と器械点の三角形から器械点の座標値を求めていきます。
今回使用した公式は「正弦定理」「余弦定理」「三平方の定理」「三角関数」「円に接する四角形の性質」の5つになります。
後方交会法は土工事などの現場測量に利用して、正確さを要する構造物などの測量は、座標点に器械を据え付けて測量するようにしましょう。
皆様の参考になれば幸いです。
 にほんブログ村 |
 にほんブログ村 |
 にほんブログ村 |
ABOUT ME
川下政明（かわしもまさあき）と申します。
土木施工管理歴３０年。
地場の建設会社に勤務しております。
1級土木、2級管工事、2級舗装、測量士、採石業務管理者を保有しております。
このブログは、工事現場に関する「施工管理」・「測量」・「HO_CAD」・「JW-CAD」・「パソコン」などについて発信しています。
参考にしていただけると嬉しいです。
土木施工管理歴３０年。
地場の建設会社に勤務しております。
1級土木、2級管工事、2級舗装、測量士、採石業務管理者を保有しております。
このブログは、工事現場に関する「施工管理」・「測量」・「HO_CAD」・「JW-CAD」・「パソコン」などについて発信しています。
参考にしていただけると嬉しいです。
