【土方カーブ】の計算方法｜三角関数で計算した数値と比較してみた

このブログでは、「土方カーブ」の計算方法と、「土方カーブって本当に正しいの？」ということで三角関数で計算した数値と比較したものについて解説いたします。

結論として、土方カーブは三角関数で計算した数値やCADで計測した数値と合いません。

土方カーブ公式

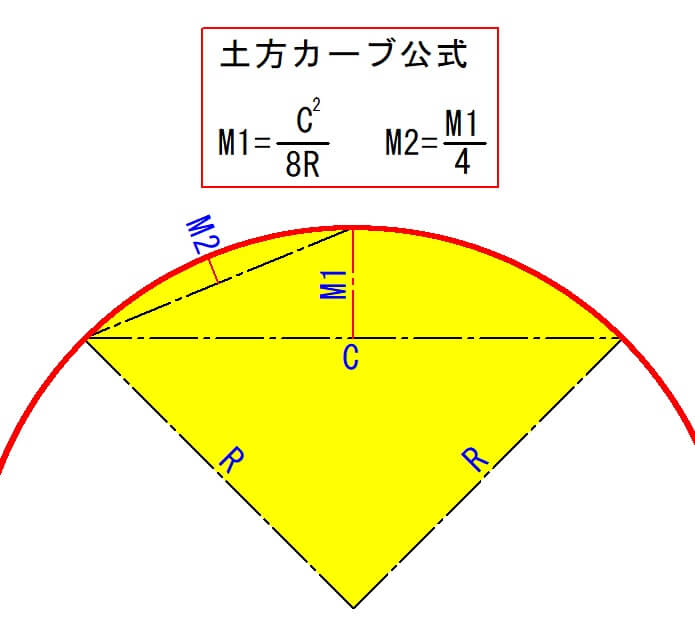
例として、R=100m、C=100mを入力して【M1】を計算します。

$$\frac{C^2}{8R}=M1$$
$$\frac{100^2}{8×100}=M1$$
$$M1＝12.500ｍ$$

算出したM1をもとに、【M2】を計算します。

$$\frac{M1}{4}=M2$$
$$\frac{12.500}{4}=M2$$
$$M2＝3.125m$$

三角関数で確認する

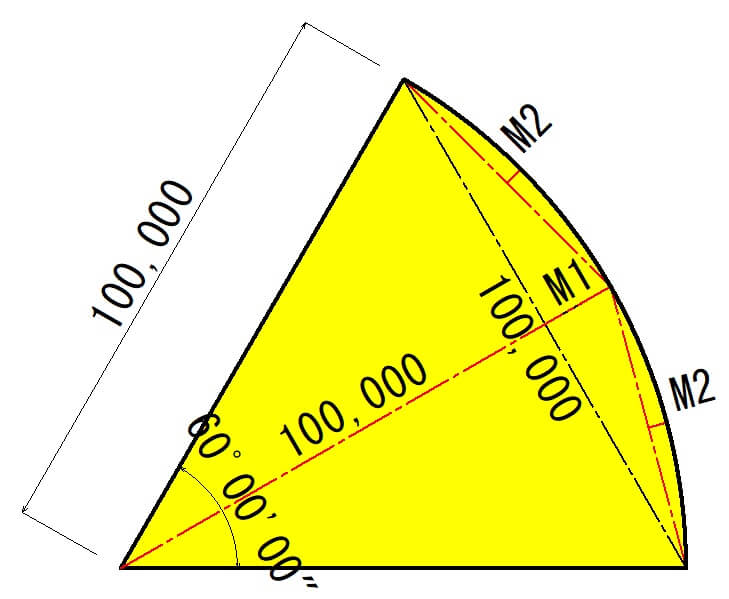
先ほどと同じ条件の、R=100m、C=100mで計算してみます。
1辺が100mの正三角形になります。

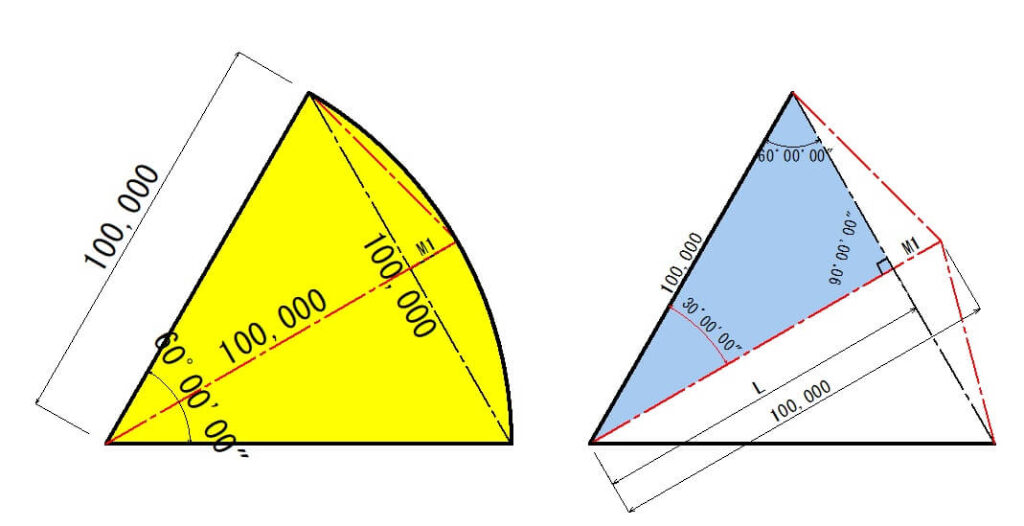
M1の確認方法として、右側の青い三角形から「L」を計算して、R=100.0mから引算します。
M1＝R-L

最初に角度「θ＝30度」の確認をしてみましょう。
1/2C＝50.0mをもとに計算します。

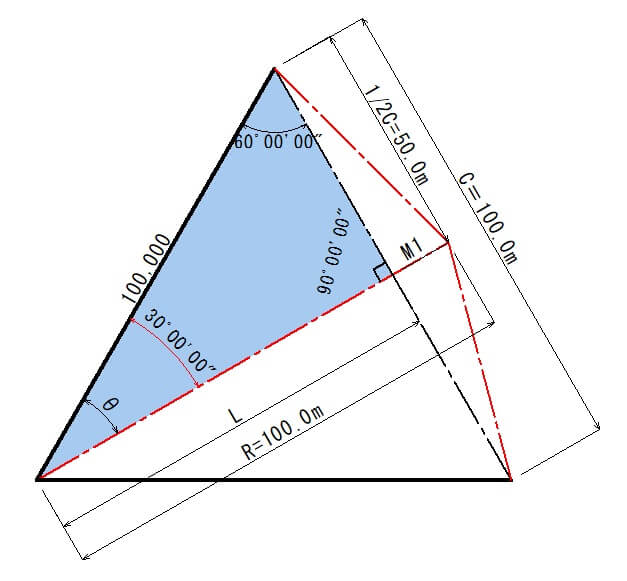
$$sinθ=\frac{50.0}{100.0}$$
$$θ=30°00′$$
θ＝30度を確認することができました。

Lを計算します。
$$cos30°=\frac{L}{100.0}$$
$$L=86.603$$

R=100.0mから引算します。
M1＝R-L
$$M1=100.0-86.603$$
$$M1=13.397$$

したがって、三角関数で計算するとM1＝13.397mとなり、土方カーブで計算したM1＝12.500ｍと0.897mもの差があることが分かります。

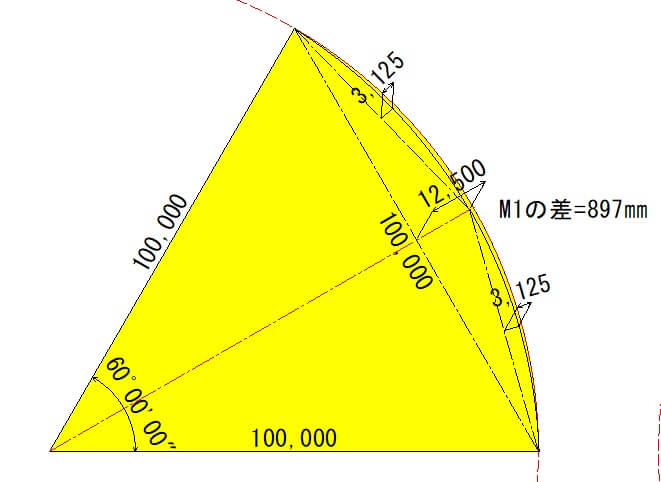
R＝100.0ｍでθ15度刻みでＭ１を比較

土方カーブ「M1」と三角関数「M1」を比較した結果、土方カーブはM1の数値が小さくなってしまうことが分かりました。

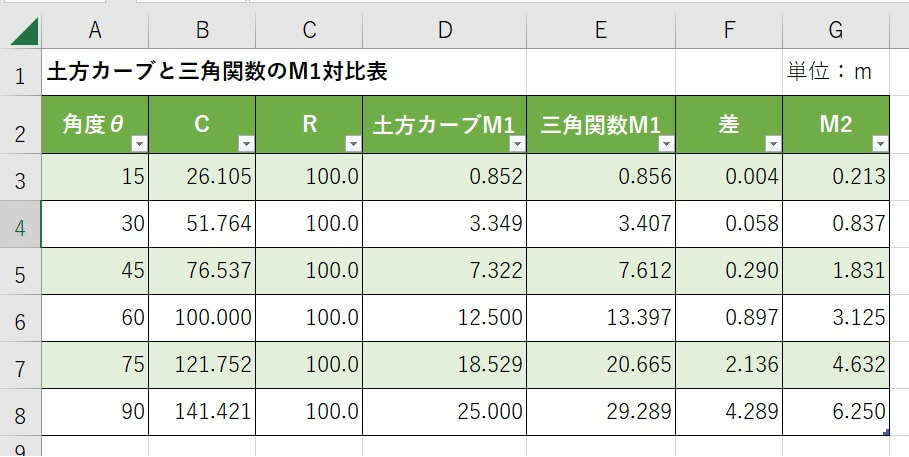
CAD上でM1を計測した図

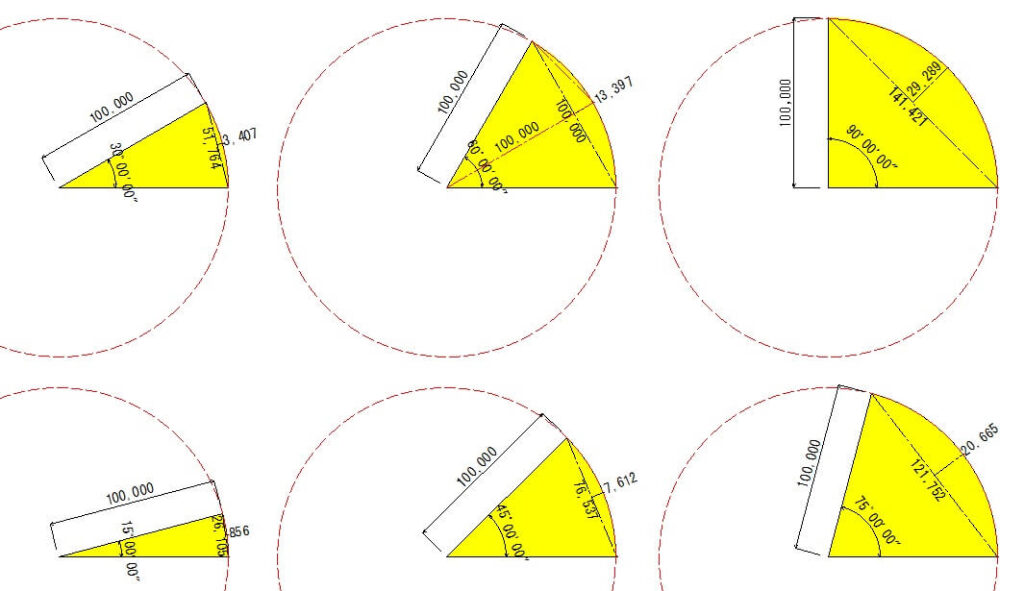
終わりに

今回のブログでは、土方カーブの計算方法と、実際に合っているのかを確認してみました。

土方カーブは、三角関数で計算した数値と合いません。
そして、CAD上で計測しても、土方カーブの数値にはなりません。

結論として、土方カーブは丁張と丁張の間に追加するような「C」の距離が短い場合と、「R」が大きい場合に使用するのが良いと思われます。
曲線丁張の見た目がよければ「OK」という場合にのみ使いましょう。

最後までお読みいただきありがとうございました。

にほんブログ村

にほんブログ村

にほんブログ村

施工管理技士・受験対策通信講座「独学サポート事務局」申込促進プロモーション

独学サポート事務局

川下　政明

土木施工管理技士

TwitterInstagramYouTube

川下政明（かわしもまさあき）と申します。
土木施工管理歴３０年。
地場の建設会社に勤務しております。
1級土木、2級管工事、2級舗装、測量士、採石業務管理者を保有しております。
このブログは、工事現場に関する「施工管理」・「測量」・「HO_CAD」・「JW-CAD」・「パソコン」などについて発信しています。
参考にしていただけると嬉しいです。