トランシットの【対回観測】そして【方向観測法】を解説|測量学

トランシットやトータルステーションを使った【対回観測】と【方向観測法】の測定方法について解説します。
参考文献はこちらです。
教程「基準点測量」 山海堂
望遠鏡正位、反位の観測
トランシットの望遠鏡は水平軸の周りを自由に回転します。
鉛直目盛版の右側に望遠鏡が置かれた状態を「望遠鏡正位」、その反対を「望遠鏡反位」といいます。
基準点測量においては望遠鏡正位、反位の観測をするのが原則となります。
この望遠鏡正位、反位の観測によって視準線の傾き、水平軸の傾き、目盛盤の偏心、視準線の偏心の影響が除かれます。


対回観測(ついかいかんそく)
望遠鏡正位、反位の観測1組を1対回観測といいます。
測量の目的精度に応じて2対回、3対回・・・の観測をします。
この場合180度/n(nは対回数)ずつ目盛盤の位置をずらし観測することによって、目盛盤誤差の消去をしていきます。
方向観測法
観測法
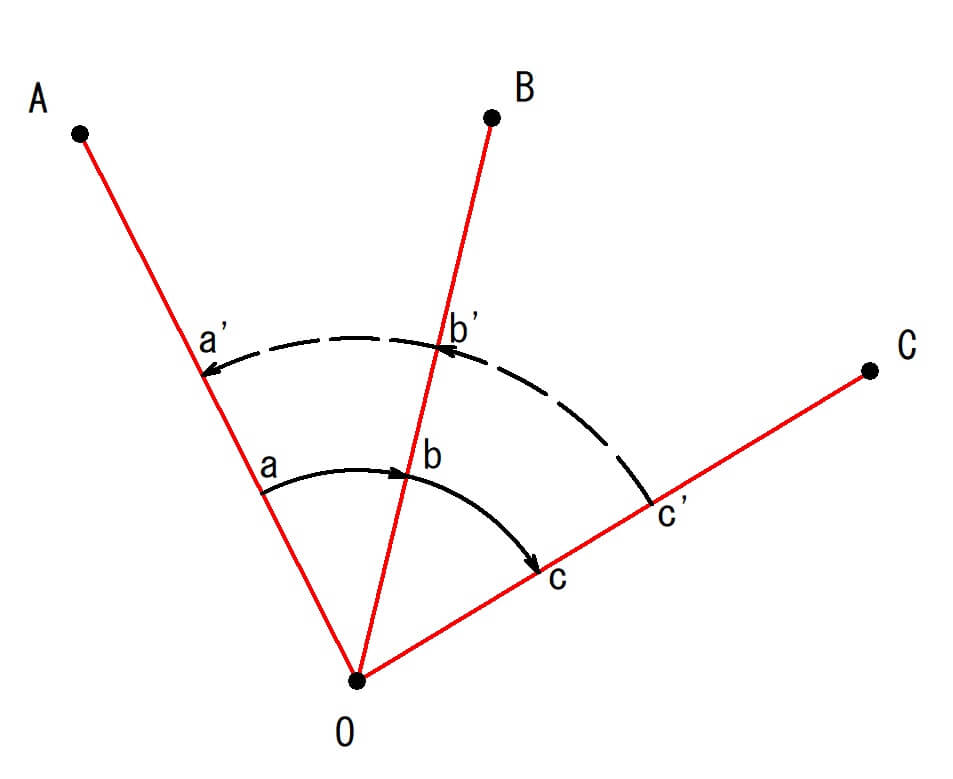
方向観測法は、複数の測点の水平角を観測するにあたり、複数測点の中の1点を基準として、順次右回りに各方向を視準します。
そして、それぞれの目盛を読取り、基準方向に基づく各方向の水平角を求める方法です。
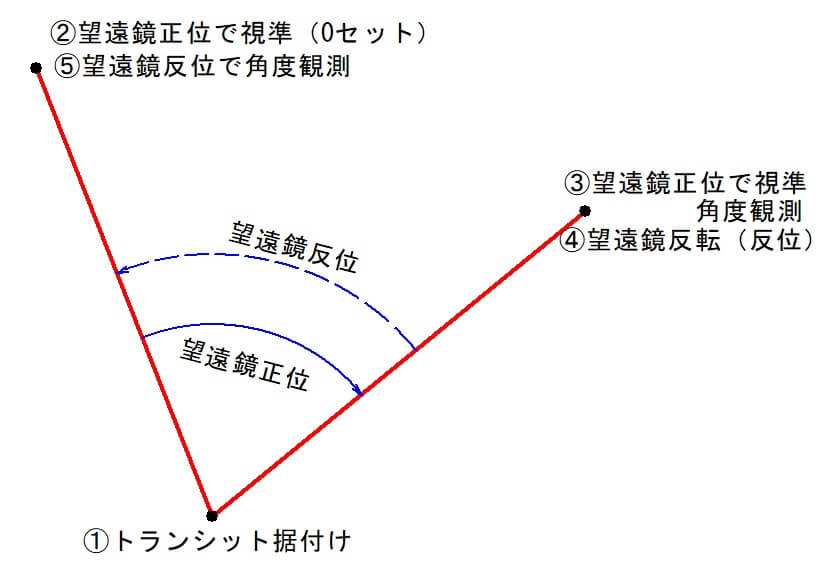
下の図は点Oにトランシットを据付けて望遠鏡正位または反位で点Aを視準し角度aを読みます。
角度aが方向OAの観測値となります。
続いて望遠鏡を右方向に回し点B,点Cの順に視準してそれぞれの観測値b,cを読みます。
次に望遠鏡を反転して(反位または正位)再び点Cを視準し、前とは逆方向に点C、点B、点Aの順に観測して各方向の観測値c’,b’,a’を読みます。
以上、望遠鏡正位、反位1組の観測で1対回の観測(方向観測)は終わりです。
対回観測と目盛変換
複数対回の観測を行う場合は、目盛の変換が伴いますので、【3対回の観測法】を例にして具体的に解説いたします。
- 望遠鏡正位(記号r)の状態で第1方向のOAを視準して、水平角度を「0セット」します。
A→B→Cと順に視準・観測します。
続いて望遠鏡を反転して前と逆の順でC→B→Aのように視準・観測します。
これで第1対回(目盛盤0°)は終わりです。 - 第2対回は、望遠鏡反位(記号ℓ)のままで第1方向OAを視準して水平角を240°(望遠鏡正位で60°)「180°/n=180°/3=60°」に合わせA→B→Cを視準・観測した後、望遠鏡を反転し望遠鏡正位(記号r)にして逆順で視準・観測します。
これで第2対回は終わりです。
このとき第1方向の角度は60°を示すはずです。 - 第3対回は、望遠鏡正位(記号r)の状態で第1方向を120°に合わせて観測を始め第3方向まで測り、望遠鏡を反転して第1方向に戻り観測が終了します。
以上で3対回(0°60°120°)の観測は終わりです。
方向観測において組み合わせた1組の方向(今回の場合は3方向)を1連列といいます。
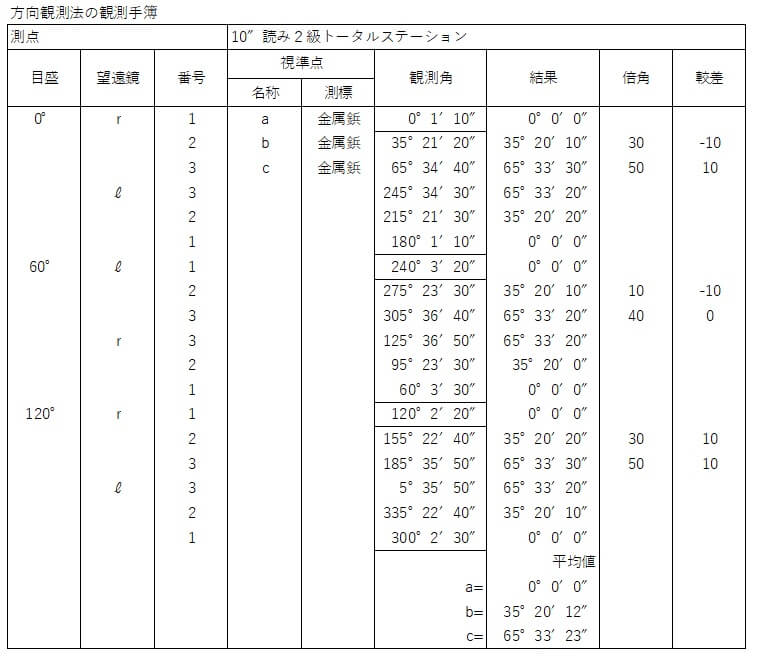
方向観測の手簿
3方向、3対回観測の記載についてお話しします。
各方向の観測値は「観測角」欄に記載されています。
「結果」欄は各対回それぞれの観測角から基準方向(零方向)の観測角を引いたもので、この場合零方向を基準とした各方向の観測角になります。
最右列の倍角、較差(かくさ)は観測値の点検のためのものです。
倍角差・観測差
方向観測によって得られた「結果」欄は、誤差がなければ同一方向の6個の値は一致するのですが、実際の観測ではトランシットの器械誤差や視準・設定に伴う観測誤差などを含むために一致しないのが普通です。
倍角差、観測差はこのような観測値の良否の判定に用いられます。
倍角差、観測差の計算に先立ち、まず倍角、較差の計算を行います。
- 「倍角」は、ある方向について1対回の望遠鏡正位、反位の観測値の和となります。
- 「較差」は、正位と反位との差になります。
上の手簿での第2方向「b」倍角は、
- 目盛位置0°のとき「30″」
- 目盛位置60°のとき「10″」
- 目盛位置120°のときは「30″」
となっていて、較差は-10″,-10″、10″となりました。
倍角差は全対回の最大値と最小値の差となるので、
倍角差=30″ー10″=20″
となります。
観測差は全対回の較差の最大値と最小値の差となるので、
観測差=+10″-(-10″)=+20″
となります。
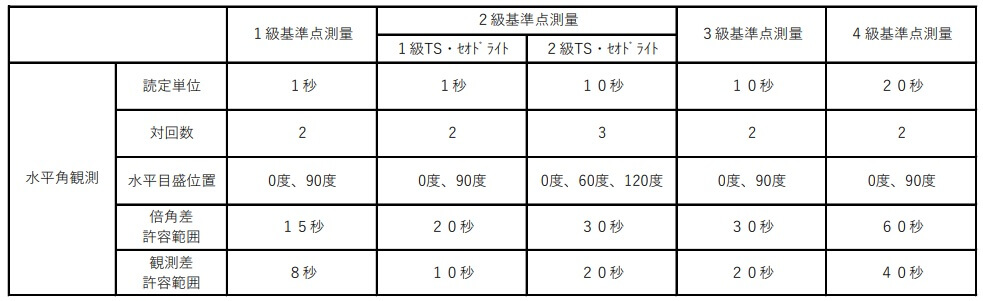
作業規定では使用するトランシットの性能及び観測対回数に応じて倍角差、観測差の制限が定められていて、これを超えたものは再測となります。
観測上の注意
1連列の組み合わせ方向数を多くしないことと、観測時間が長引けばトランシットの変動や気象の変化が大きくなるので、各級の基準点測量では、1連列の方向数に上限を設けています。
- 1級基準点測量:4辺以内
- 2級基準点測量:5辺以内
- 3級基準点測量:7辺以内
- 4級基準点測量:10辺以内
方向数が多い為に2連列以上に分けるときは、同1連列に距離があまり違わないものを選ぶのがよいでしょう。
分けた各連列には必ず同じ基準方向を含めることと、0方向(基準方向)は、目標がよく見える方向、組み合わせる方向の中で平均距離に近い方向、観測点の高次点になる方向を選びます。
方向観測法の特徴
方向観測法は、現在最も多く採用されている測角法で、その特徴は次の通りです。
- 方向の観測を行う。
- もっとも能率が良い測角法。
- 望遠鏡正位・反位の観測による器械誤差の消去・対回観測による目盛の変換等が巧みに組み合された合理的観測法。
- 倍角差・観測差を用いて観測の良否の判定ができる。
おわりに
今回のブログでは、「対回観測」方向観測法について解説させていただきました。
水平角の測定は「対回観測」が基本となります。
方向観測法は、1点のまわりに多数の「角」があるときに用いられる方法で、対回観測の応用となります。
そして、公共測量作業規定では、この方向観測法を使うこととなっております。
以上となります。
最後までお読みいただきありがとうございました。

|
にほんブログ村 |
にほんブログ村 |
にほんブログ村 |