三角関数【sin,cos,tan】の覚え方と計算方法のおさらい

今回のブログでは、測量の計算で使う「sin、cos、tan」の覚え方と計算方法についてお話しします。

三角関数は、直角三角形の三辺の比率のことを言います。

こちらが三角関数を覚える際によく見かける図形です。

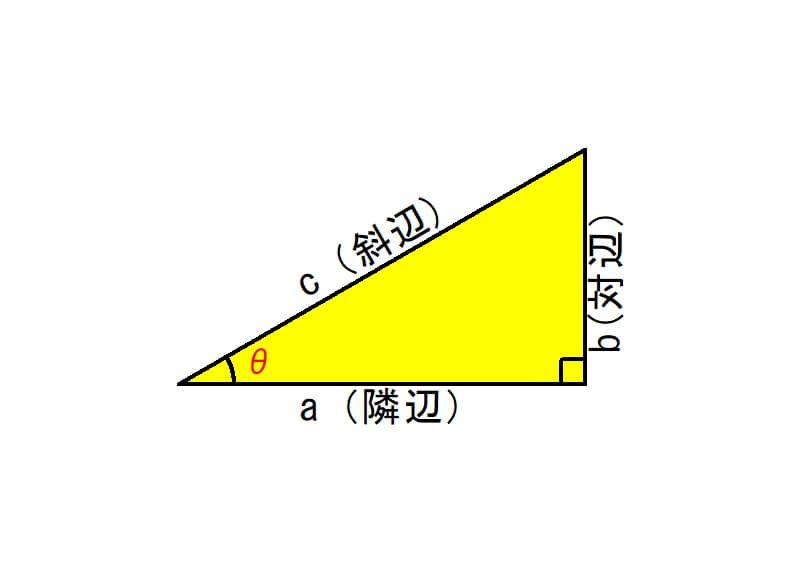
$$sinθ=\frac{b}{c}$$

$$cosθ=\frac{a}{c}$$

$$tanθ=\frac{b}{a}$$

平面直角座標をイメージするとこのような図形になります。

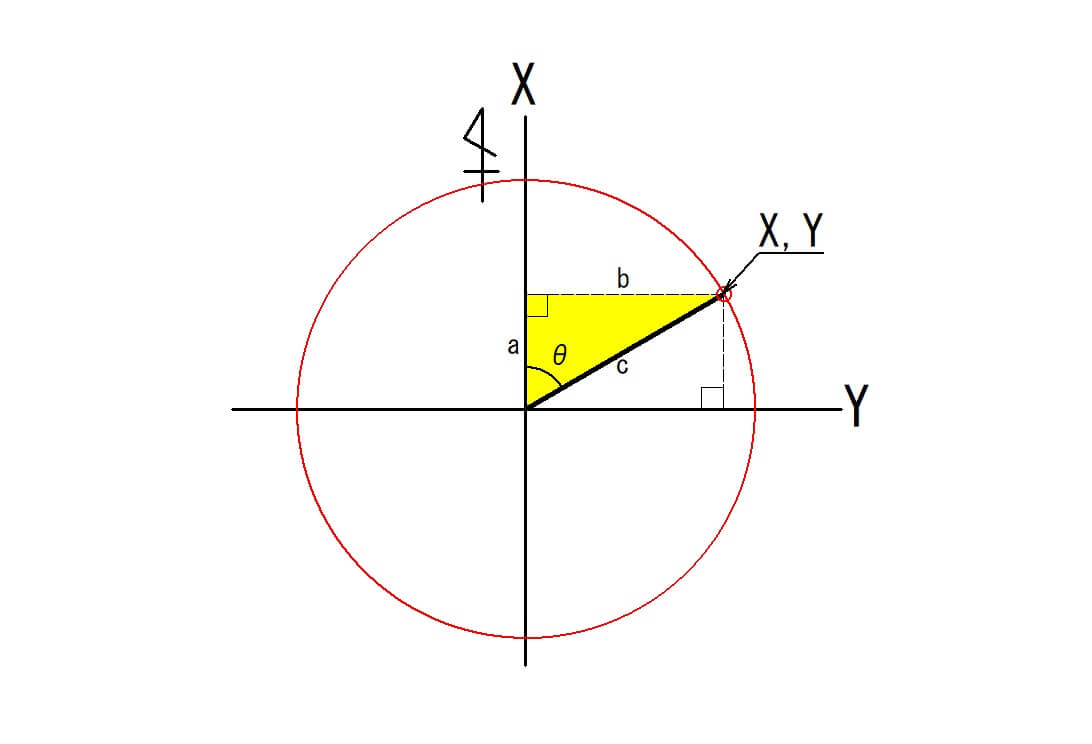
しかし、この図形だけで三角関数を覚えてしまうと、下の図な場合、少し悩んでしまいますね。

【tan】から覚えてみよう

tanは、θから伸びる水平直角の【辺】の割合なので、「差金」をイメージすると覚えやすい(個人的感覚）。

$$tanθ=\frac{b}{a}$$

縦線と横線、横線と縦線といった感じで斜辺を使わない辺の割合がtanです。

【cos】と【sin】は斜辺が分母

tan以外の【sin】・【cos】は「斜辺」が分母となります。

分子が「対辺」の場合【sin】、「隣辺」の場合【cos】になります。

$$cosθ=\frac{a}{c}$$

$$sinθ=\frac{b}{c}$$

【cos】はアルファベットの「C」

やはりコサインの「C」で覚えるのが定番ですね。

θを「C」で覆いかぶせるように挟みます。

分母が斜辺「c」、分子が隣辺「a」です。

$$cosθ=\frac{a}{c}$$

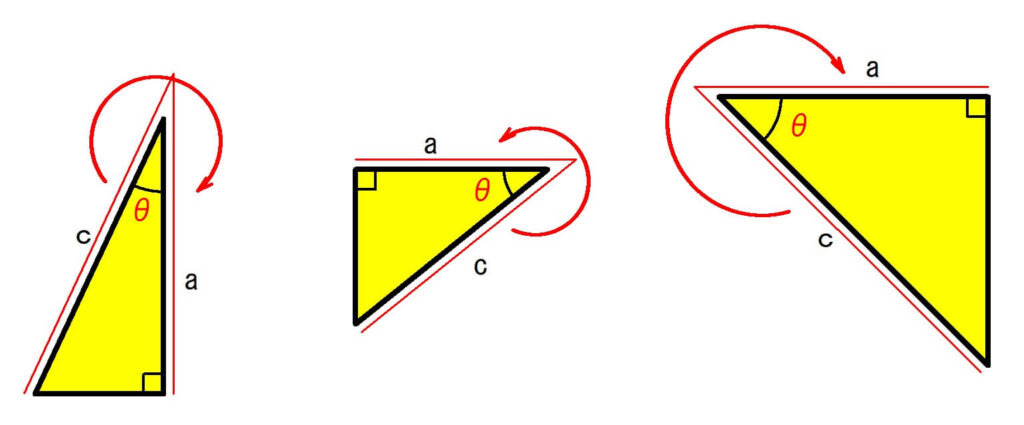
【sin】はtanをひっくり返すイメージ

タンジェントは「差金」をイメージするといったお話をしましたが、その「差金」パタン！と反対側へひっくり返した「とんがり帽子」のようなイメージだと覚えやすいと思います。

$$sinθ=\frac{b}{c}$$

練習問題

１問目

下の直角三角形の「b」と「c」を関数電卓を使って計算してみよう。

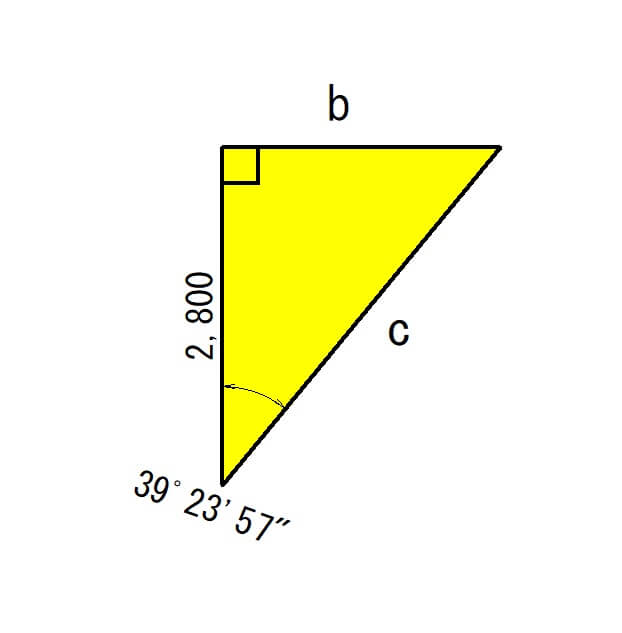
bの計算

「b」から計算してみましょう。

垂直水平辺から求められるので「差金」ですね。

タンジェント「tan」を使います。

$$tanθ=\frac{b}{a}$$

$$tan39°23′57″=\frac{b}{2.800}$$

$$0.821384903=\frac{b}{2.800}$$

$$ｂ=2.2998777≒2.300$$

cの計算

「c」を計算してみましょう。

角度を覆いかぶせるアルファベットの「C」をイメージできるので、コサイン「cos」を使います。

$$cosθ=\frac{a}{c}$$

$$cos39°23′57″=\frac{2.800}{c}$$

$$0.772742805=\frac{2.800}{c}$$

$$c=3.623456577≒3.623$$

2問目

次のにこちらの図形で計算してみましょう。

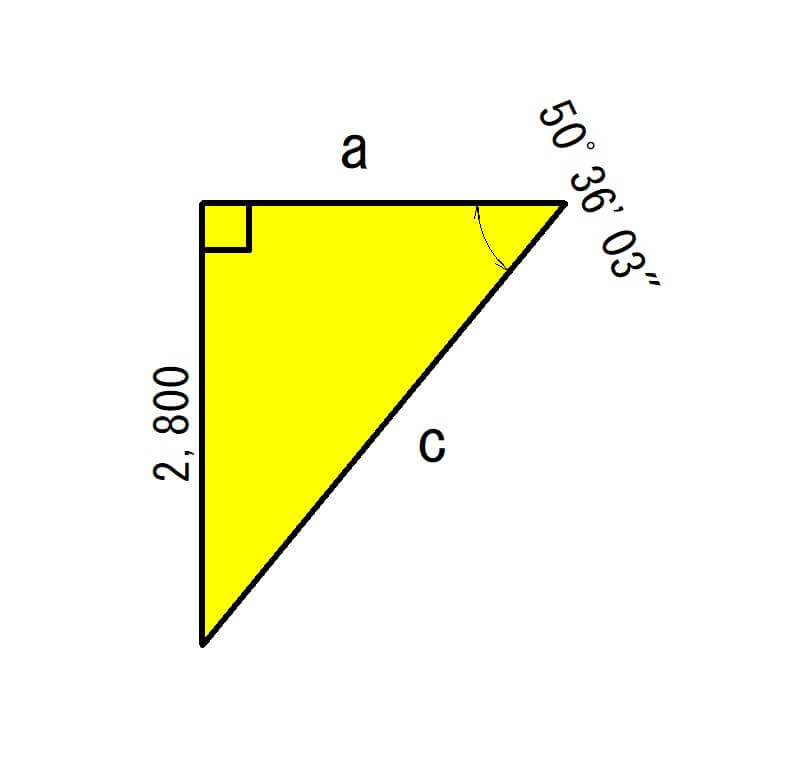
aの計算

「a」から計算してみましょう。

これも垂直水平辺から求められるので「差金」ですね。

タンジェント「tan」を使います。

$$tanθ=\frac{b}{a}$$

$$tan50°36′3″=\frac{2.800}{a}$$

$$1.217456026=\frac{2.800}{a}$$

$$a=2.2998777≒2.300$$

cの計算

最後に「c」を計算してみましょう。

「差金」パタン！と反対側へひっくり返した「とんがり帽子」のようなイメージなのでサイン「sin」を使います。

$$sinθ=\frac{b}{c}$$

$$sin50°36′3″=\frac{2.800}{c}$$

$$0.772742805=\frac{2.800}{c}$$

$$c=3.623456577≒3.623$$

まとめ

今回のブログでは「三角関数」の【sin,cos,tan】の覚えたかと計算方法について解説させていただきました。

$$sinθ=\frac{b}{c}$$

$$cosθ=\frac{a}{c}$$

$$tanθ=\frac{b}{a}$$

• tanは、θから伸びる水平直角辺の割合なので、「差金」をイメージすると覚えやすいです。
• tan以外の【sin】・【cos】は「斜辺」が分母となります。
• cosはコサインの「C」でθを覆いかぶせるようなイメージです。
• sinはtanの「差金」をパタン！と反対側へひっくり返した「とんがり帽子」のようなイメージ、というのと「tanとcos以外」というので覚えられるかなと思います。

以上となります。

最後までお読みいただきありがとうございました。

にほんブログ村

にほんブログ村

にほんブログ村

川下　政明

土木施工管理技士

XInstagramYouTube

川下政明（かわしもまさあき）と申します。
土木施工管理歴３０年。
地場の建設会社に勤務しております。
1級土木、2級管工事、2級舗装、測量士、採石業務管理者を保有しております。
このブログは、工事現場に関する「施工管理」・「測量」・「HO_CAD」・「JW-CAD」・「パソコン」などについて発信しています。
参考にしていただけると嬉しいです。